第一章 - AVL 树和伸展树

约 1460 个字预计阅读时间 5 分钟

AVL 树

AVL 树 (Adelson-Velsky and Landis tree) 是带有平衡条件的二叉查找树。具体地说，一棵 AVL 树是其每个节点的左子树和右子树的高度最多差 \(1\) 的二叉查找树。

基于这个性质，记高度为 \(h\) 的 AVL 树的最少节点数为 \(S(h)\)，则容易得到 \(S(0) = 1, S(1) = 2, S(h) = S(h - 1) + S(h - 2) + 1\) 这样的递推关系。即根的左子树和右子树分别是高度为 \(h - 1\) 和 \(h - 2\) 的两棵 AVL 树。

因此除去插入操作外，所有的树操作都可以在 \(O(\log N)\) 内完成。而插入操作的困难在于，简单的二叉查找树插入可能会破坏 AVL 树的特性，因此在插入后还需要对树进行修正，这个操作称作旋转 (rotation)，这也是 AVL 树的核心操作。

在插入后，只有从插入点到根节点的路径上的节点平衡可能被改变。我们将从深到浅地在这条路径上，找到第一个（即最深的）不满足 AVL 条件的节点。可以意识到，使这个节点及其子树重新满足 AVL 条件，即可使整棵树重新满足 AVL 条件。

那么我们将这个节点记作 \(\alpha\)，其左右子树的高度差为 \(2\)。于是这种不平衡可以分为以下 4 种情况：

对 \(a\) 的左子节点的左子树进行了一次插入。
对 \(a\) 的左子节点的右子树进行了一次插入。
对 \(a\) 的右子节点的左子树进行了一次插入。
对 \(a\) 的右子节点的右子树进行了一次插入。

不难意识到，情形 1 和 4 是对称的，称作「外部」情形；情形 2 和 3 也是对称的，称作「内部」情形。前者通过单旋 (single rotation) 完成，后者通过双旋 (double rotation) 完成。

单旋

介绍单旋，我们将以情形 1 进行介绍，即如下图：

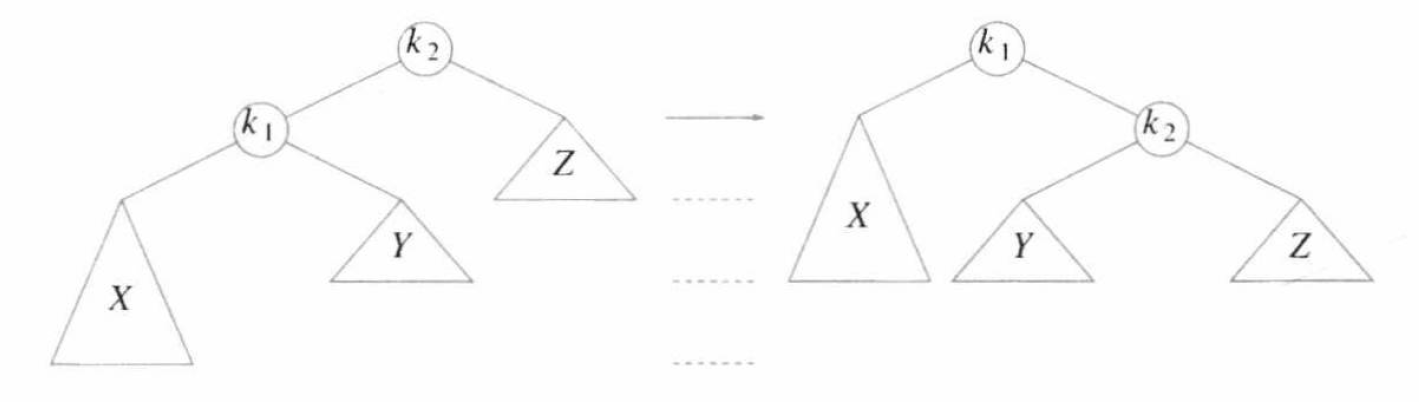
为使树恢复平衡，我们将 \(X\) 上移一层，将 \(Z\) 下移一层。更具体的来说，此时 \(k_2\) 是我们的目标节点 \(\alpha\)。我们使其较大子树的根节点 \(k_1\) 取代自己成为新的根，然后 \(k_2\) 自己成为 \(k_1\) 的右子节点，并使原本 \(k_1\) 的右子树成为 \(k_2\) 的左子树。

对于对称的结构，只需对称进行操作即可。

双旋

介绍单旋，我们将以情形 2 进行介绍，即如下图：

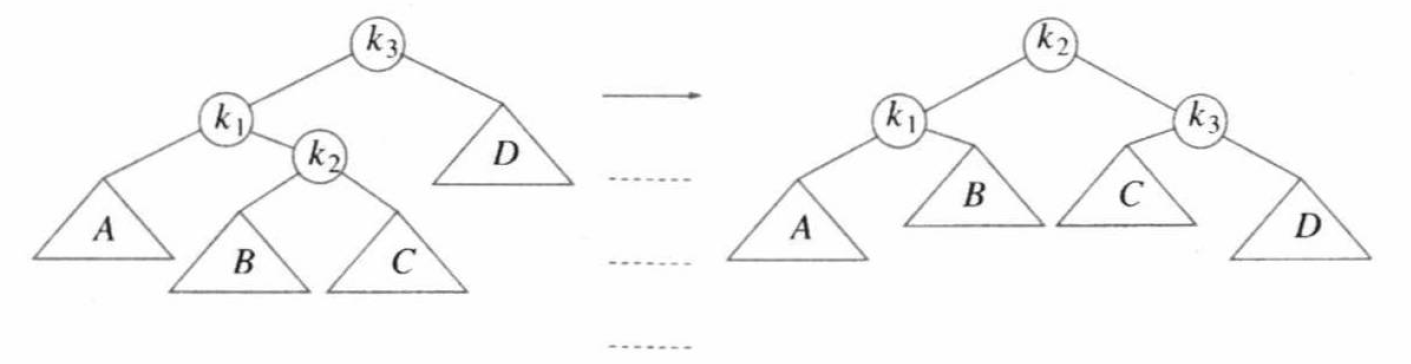
为使树恢复平衡，我们将 \(B, C\) 都需要上移一层，将 \(D\) 下移一层。更具体的来说，此时 \(k_3\) 是我们的目标节点 \(\alpha\)。我们使其较大子树的根节点 \(k_1\) 的较大子树的根节点 \(k_2\) 取代自己成为新的根，然后 \(k_3\) 自己成为 \(k_2\) 的右子节点，并使原本 \(k_2\) 的左子树成为 \(k_1\) 的右子树，原本 \(k_2\) 的右子树成为 \(k_3\) 的左子树。

由于该操作可以由两次单旋操作完成，即对 \(k_1\) 做一次左单旋，再对 \(k_3\) 做一次右单旋，所以称作双旋。

对于对称的结构，只需对称进行操作即可。

具体实现

在具体的代码实现中，我们需要用一个量来表征树的平衡情况。常用的这个量是平衡因子 (balance factor)，定义为节点左子树的高度减右子树的高度之差。因此对于 AVL 树来说，每个节点的平衡因子取值只能是 \(-1, 0, 1\)。

因此，在每次插入操作后，我们会递归地更新新节点到根节点路径上所有节点的平衡因子，并找出其中第一个值不为 \(-1, 0, 1\) 的节点作为目标节点，根据其左右子树情况作对应的旋转操作即可。

伸展树

伸展树 (splay tree) 是一种相对简单的平衡树。其低复杂度不取决于单独每次操作的低复杂度，而是取决于连续多次操作的低均摊 (amortised) 复杂度。具体来说，其保证任意连续 \(M\) 次对树的操作复杂度最多为 \(O(M \log N)\)。但是其不保证任意单独一次操作的复杂度，即其中的单独一次操作有可能需要 \(O(N)\) 的复杂度。

伸展树的基本想法是，当一个节点被访问后，其就要经过一系列旋转操作被放到根上。在此过程中，其原路径上的所有节点的深度也会降低，从而起到平衡的效果。而且由于操作的唯一性，伸展树不需要额外的信息（如平衡因子）就可以实现。

但是这个旋转操作，并不是简单的一直单旋就可以降低均摊复杂度的。取而代之的，我们采用的是展开 (splaying) 操作，这也是伸展树的核心操作。

展开

对于要进行展开操作的节点 \(X\)，我们记其父节点和祖父节点分别为 \(P\) 和 \(G\)。当然有一种情况是 \(G\) 不存在，这样只需要一次单旋就可以将 \(X\) 换至根上。除此之外，我们需要分两种情况讨论。

Zig-Zag

Zig-Zag 情形如下图：

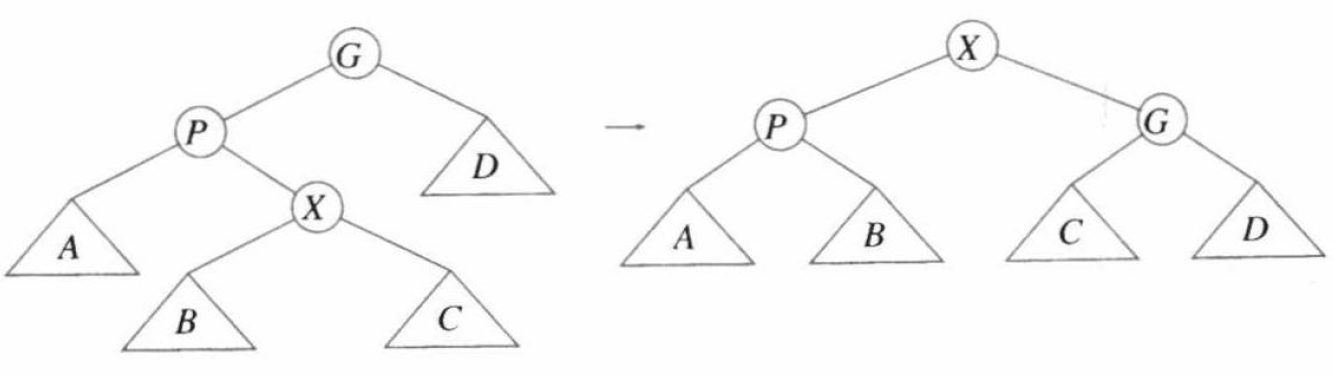
此时我们只要进行双旋即可。对称的情况作对称处理。

Zig-Zig

Zig-Zig 情形如下图：

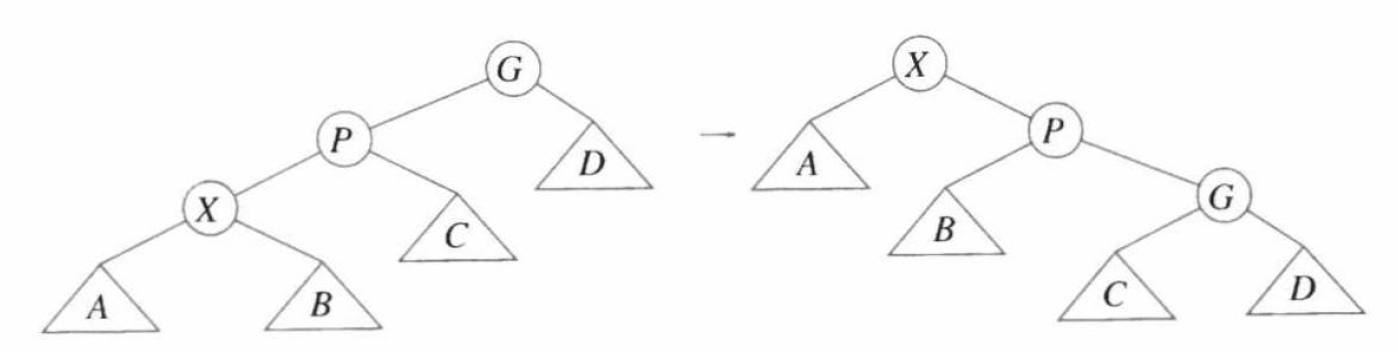
此时我们先对祖父节点 \(G\) 作一次单旋，再对父节点 \(P\) 作一次单旋。请注意！这与双旋的区别在于，这两次单旋的操作是先浅后深的，与双旋相反。对称的情况作对称处理。