第三章 - 优先队列(堆)
约 2611 个字 预计阅读时间 9 分钟
在数据结构基础 - 第四章 - 优先队列(堆)中,我们已经较为详细地讨论了「堆」这一数据结构。
但是我们也留下了一个问题,即一般的堆是难以合并的。以二叉堆为例,一个可行的合并方式是先将两个堆的数组拼接,然后采用线性建堆的方式,即从树的倒数第二层开始,对每一层的每一个节点执行下滤操作完成合并。容易直到这样操作的复杂度是线性的,这不够高效。
为了解决这个问题,我们将介绍几种高级的堆数据结构,来解决这一问题。
左式堆
左式堆 (leftist heap) 也是满足堆序性的二叉树。但是相较一般的二叉堆,左式堆不仅不趋向理想平衡 (perfectly balanced),而且实际上的趋向于非常不平衡的。在具体构建这一数据结构前,我们需要引入一些概念。
左式堆的性质
我们将任意节点 \(X\) 的零路径长 (Null Path Length, NPL) \(\texttt{Npl} (X)\) 定义为从 \(X\) 到一个没有两个子节点的节点的最短路径长。
因此,具有 0 个或 1 个子节点的节点的 \(\texttt{Npl}\) 为 \(0\),\(\texttt{Npl}(\texttt{NULL}) = -1\)。同时一个重要的性质是,任意节点的零路径长比其所有子节点的零路径长的最小值多 \(1\)。
左式堆的性质是:对于堆中的每一个节点 \(X\),左子节点的零路径长不小于右子节点的零路径长。显然这一性质会使得树偏向于向左增加深度,这也是其得名的由来。
进一步地,在右路径上有 \(r\) 个节点的左式堆必然至少有 \(2^{r} - 1\) 个节点。换言之,有 \(N\) 个节点的左式堆右路径最多含有 \(\lceil \log (N + 1) \rceil\) 个节点。因此对左式堆操作的一般思路是将所有工作放到右路径上进行。于是我们关注的是,如何在对右路径进行插入和合并操作后恢复左式堆的性质。
左式堆的操作
对左式堆的基本操作是合并。具体来说我们这样操作:
- 比较两个左式堆的根节点,取较小的节点作为新堆的根,其左子树作为新堆的左子树;
- 递归地合并较小节点的右子树和另一个堆,更新根节点的零路径长(即为右子节点的零路径长加 \(1\));
- 如果合并完成后,右子树的零路径长大于左子树,则交换左子树和右子树。
执行合并的时间与右路径的长的和成正比,因为在递归调用期间对每一个被访问的节点执行的是常数工作量,因此合并两个左式堆的时间复杂度为 \(O(\log N)\)。
特别地,对左式堆插入一个新节点可以看作是向原堆合并一个单节点堆。
左式堆中删除最小值是容易的,只需要合并根节点的左右子堆即可。
斜堆
斜堆 (skew heap) 是左式堆的自调节形式,实现起来较为简单。斜堆自身在结构上只要求保证堆序性,而不作类似于左式堆对零路径长等性质的要求。
斜堆的操作
能做到这一点的核心也在于斜堆的合并操作。具体来说,我们做以下操作:
- 比较两个左式堆的根节点,取较小的节点作为新堆的根,其左子树作为新堆的左子树;
- 递归地合并较小节点的右子树和另一个堆,更新根节点的零路径长(即为右子节点的零路径长加 \(1\));
- 合并完成后,总是交换左子树和右子树。
可以看到,斜堆与左式堆的差异仅在于何时交换左右子树,在斜堆中交换是无条件的。
斜堆的复杂度分析
对于斜堆操作的复杂度,我们先给出结论。因为斜堆的右路径在任意时刻都可以任意长,所以所有操作的最坏情形运行时间都是 \(O(N)\)。
但是令人惊异的是,斜堆的操作可以保证对任意 \(M\) 次连续操作,总的最坏情形运行时间是 \(O(M \log N)\)。因此斜堆每次操作的均摊复杂度是 \(O(\log N)\)。这一结论需要均摊分析加以证明。
Proof
先给出一些定义:
- 轻结点:右子树节点数不大于左子树节点数的节点。
- 重结点:右子树节点数大于左子树节点数的节点。
- 势能函数 \(\Phi (i)\):第 \(i\) 次合并后,堆的重结点数。
设总共进行 \(M\) 次合并,斜堆的节点数始终不大于 \(N\)。
考察第 \(i\) 次操作,合并堆 \(H_{1}\) 和 \(H_{2}\)。记堆 \(H_{1}\) 右路径上有 \(l_{1}\) 个轻节点、\(h_{1}\) 个重节点;堆 \(H_{2}\) 右路径上有 \(l_{2}\) 个轻节点、\(h_{2}\) 个重节点。那么这次合并的实际开销
合并完成后,右路径上原本的重结点一定会变为轻节点,因为其本身右子树比左子树节点数多,且合并又发生在右子树上,于是交换左右子树后该节点的左子树一定比右子树节点数多。而轻节点是否变为重结点是不好确定的,于是我们考虑最坏情况,即所有轻节点都变为重结点。那么本次合并的势能变化
均摊开销等于实际开销加势能变化,即
于是全部 \(M\) 次操作的均摊开销为
又考虑到 \(\Phi_{0}, \Phi_{M} \in [0, N]\),于是
于是每次操作的均摊复杂度即为 \(O(\log N)\)。
二项队列
二项队列结构
二项队列 (binomial queue) 是若干堆序树的集合,称作森林 (forest)。堆序树中的每一棵都是有约束的形式,称作二项树 (binomial tree)。每一个高度上至多存在一棵二项树。高度为 \(0\) 的二项数是一棵单节点树,高度为 \(k\) 的二项树 \(B_{k}\) 通过将一棵二项树 \(B_{k - 1}\) 接到另一棵二项树 \(B_{k - 1}\) 的根上构成。下图展示了 \(B_{0}, B_{1}, B_{2}, B_{3}, B_{4}\)。
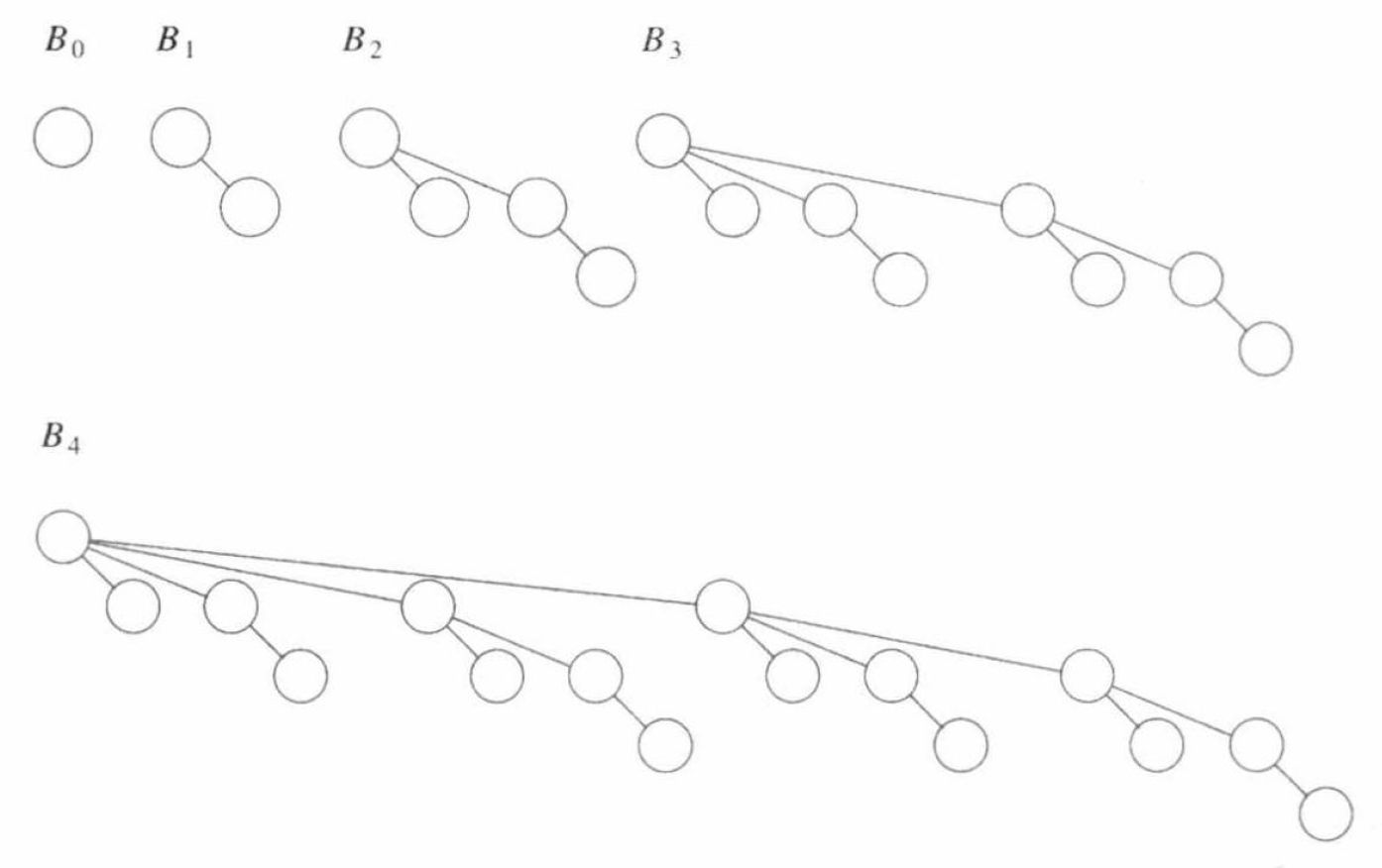
可以看到,二项树 \(B_{k}\) 由一个带有 \(B_{0}, B_{1}, \cdots, B_{k - 1}\) 的根节点组成。高度为 \(k\) 的二项树恰好有 \(2^{k}\) 个节点,而在深度 \(d\) 处的节点数是二项系数 \({k \choose d}\)。于是,对于任意大小为 \(N\) 的优先队列,可以由森林 \(B_{m_{0}}, B_{m_{1}}, \cdots, B_{m_{k}}\) 表示,其中 \(m_{0}, m_{1}, \cdots, m_{k}\) 为 \(N\) 在二进制表示下值为 \(1\) 的位对应大小的二项树。这便满足了二项队列的定义。
二项队列操作
根据如上的构造,可以知道对于大小为 \(N\) 的优先队列,最多有 \(\log N\) 棵不同的树。因此最小元可以通过搜索所有的树的根来找出,这一操作的复杂度即为 \(O(\log N)\)。当然,如果维护一个全局最小值并在每次插入时更新,则可以在常数时间内完成。
两棵相同高度的二项树的合并是容易的,只需要将较大的根作为子节接到较小的根上即可,故单次合并仅需常数时间。
合并两个二项队列,是通过将两个队列加到一起来完成。具体来说,如果我们要合并二项队列 \(H_{1}, H_{2}\),合并得到的二项队列为 \(H_{3}\)。按照高度从小到大,对于高度 \(d\):
- 如果 \(H_{1}, H_{2}\) 中有且仅有 1 个二项队列有高度为 \(d\) 的二项树,则将该树直接复制到 \(H_{3}\) 中;
- 如果 \(H_{1}, H_{2}, H_{3}\) 中有且仅有 2 个二项队列有高度为 \(d\) 的二项树,则将这两棵树合并得到高度为 \(d + 1\) 的二项树,复制到 \(H_{3}\) 中;
- 如果 \(H_{1}, H_{2}, H_{3}\) 中有且仅有 3 个二项队列有高度为 \(d\) 的二项树,则将其中任意两棵树(一般选用 \(H_{1}, H_{2}\) 中的)合并得到高度为 \(d + 1\) 的二项树,复制到 \(H_{3}\) 中。
Warning
在题目考察中,第三种情况的任意性往往是许多陈述「可能」正确或错误的前提,在推理时请不要忽略这一点。
因为两个二项队列总共存在 \(O(\log N)\) 棵二项树,因此两个二项队列的合并的时间复杂度仍为 \(O(\log N)\)。
插入实际上就是将仅含 \(B_{0}\) 的二项队列与原二项队列合并。但需要说明的是,向一个初始为空的二项队列进行 \(N\) 次插入操作,总的时间复杂度仅为 \(O(N)\),也就是单次插入可以达到 \(O(1)\) 的均摊复杂度。这是由二项队列的性质所决定的。
删除最小值操作也是容易的。设原优先队列为 \(H\),首先我们找出其中具有最小根的二项树 \(B_{k}\)。从 \(H\) 中删去树 \(B_{k}\) 得到优先队列 \(H'\),\(B_{k}\) 中删去根节点得到的二项树 \(B_{0}, B_{1}, \cdots, B_{k - 1}\) 构成优先队列 \(H''\)。最后合并 \(H', H''\) 即可。由于找到最小值和合并的时间复杂度都为 \(O(\log N)\),故删除最小值操作的时间复杂度仍为 \(O(\log N)\)。
二项队列的实现
为了便于操作,我们通常会将一个二项队列中所有二项树的根节点保存在一个数组中,同时使其按照从大到小的顺序保存。