第四章 - 回溯算法

约 443 个字预计阅读时间 1 分钟

回溯 (backtracking) 算法是一种常用的算法设计技巧。尽管许多情况下回溯算法相当于穷举搜索的巧妙实现，但在某些情形下，相比暴力 (brute force) 穷举搜索，其工作量也可以有显著的节省。

这一点的主要保证是通过剪枝 (pruning)，即在合适的时候删除决策树上不可行的情况，从而避免不必要的搜索。

接下来，我们会通过一些具体的方法来展示会回溯算法的应用。

收费公路重建问题

设给定 \(N\) 个点 \(p_{1}, p_{2}, \cdots, p_{N}\) 位于 \(x\) 轴上，\(x_{i}\) 是点 \(p_{i}\) 的 \(x\) 坐标。不妨设 \(x_{1} = 0\)，且 \(x_{1} < x_{2} < \cdots < x_{N}\)。这 \(N\) 个点确定在每一对点间的 \(\frac{N (N - 1)}{2}\) 个形如 \(|x_{i} - x_{j}| (i \neq j)\) 的距离。显然，给定点集，我们可以在 \(O(N^{2} \log N)\) 的时间内计算出有序的距离的集合。

收费公路重建问题 (turnpike reconstruction problem) 则是先给出距离集合，然后希望据此构造出一个合法的对应点集。

我们的算法是这样进行的：

首先我们容易得到点的数量，并且根据 \(x_{1} = 0\) 的条件，可以得到 \(x_{N}\) 的值（即最大的距离）。
接下来，我们每次取出距离集中剩余的最大距离，将其对应的点依次放在可能的合法位置上，并根据该点与其它已经固定的点的距离是否在距离集中，判断这一放法是否合法。
如果有一个合法的放置方法，就搜索下一个距离；否则回溯。

尽管这种深度搜索算法的上界都是指数级别的，我们仍然可以对其下界做一些讨论。如果我们将距离集合用平衡树维护，并且不发生回溯的话，总的时间复杂度是 \(O(N^{2} \log N)\)。这样的讨论是有意义的，因为经验表明，当点的整数坐标在 \([0, D_{\max}]\) 中均匀随机分布时，时间复杂度会大于理想下界，但仍不至达到 \(O(N^{3})\) 以及更高的阶。

博弈

接下来我们考虑一个更复杂的问题，即博弈问题。我们将以大家熟悉的井字棋 (tic-tac-toe) 为例。

在井字棋游戏中，暴力的搜索仍然是可行的，而且由于游戏规模的限制，其时间仍然是可以被接受的。但我们可以找到一些更好的方法，例如提出一个评估函数，且只搜索那些评估函数可以被接受的分支而忽略其它的，也就是基于这个值进行剪枝。

基于这一点，我们容易发现这个评估函数需要具有的一些性质：

评估函数必须能够保证算法的正确性，即不能将有正确答案的分支剪枝。
评估函数要能够有效评估局面，太弱的评估函数不能起到好的剪枝效率。
评估函数的复杂度要恰当，如果评估函数很强，但本身计算其需要很大复杂度，那么从总的算法复杂度来说是不合算的。

极小极大策略

那么在井字棋中，我们直接给出这个评估函数的构造方法。我们称作极小极大 (minimax) 策略。

在每一步下棋前，我们将棋盘上的每个位置赋值，能使计算机获胜的位置赋为 \(+1\)，平局赋为 \(0\)，使计算机输棋的位置赋为 \(-1\)。通过考察盘面能够确定这局棋输赢的位置称作终端位置 (terminal position)。

如果一个位置不是终端位置，那么该位置的值通过递归地假设双方最优棋步而确定。此时人类总希望这个值极小，而计算机总希望这个值极大。这也是「极小极大」策略得名的由来。

位置 \(P\) 的后继位置 (successor position) 是通过从 \(P\) 走一步棋可以达到的任何位置 \(P_{s}\)。如果挡在某个位置 \(P\) 计算机要走棋，那么它递归地求出所有后继位置的值。计算机选择具有最大值的一步行棋，这就是 \(P\) 的值。为了得到任意后继位置 \(P_{s}\) 的值，要递归地算出 \(P_{s}\) 的所有后继位置的值，然后选取其中最小的值，这个最小值代表行棋人一方的最优应招。

\(\alpha\) - \(\beta\) 剪枝

上面我们已经给出了基本的回溯策略，但是显然这个方法需要的时间复杂度是非常大的。于是一个重要的剪枝策略称作 \(\alpha\) - \(\beta\) 剪枝 (\(\alpha\) - \(\beta\) pruning)。

\(\alpha\) 剪枝发生在形如下例的情况：

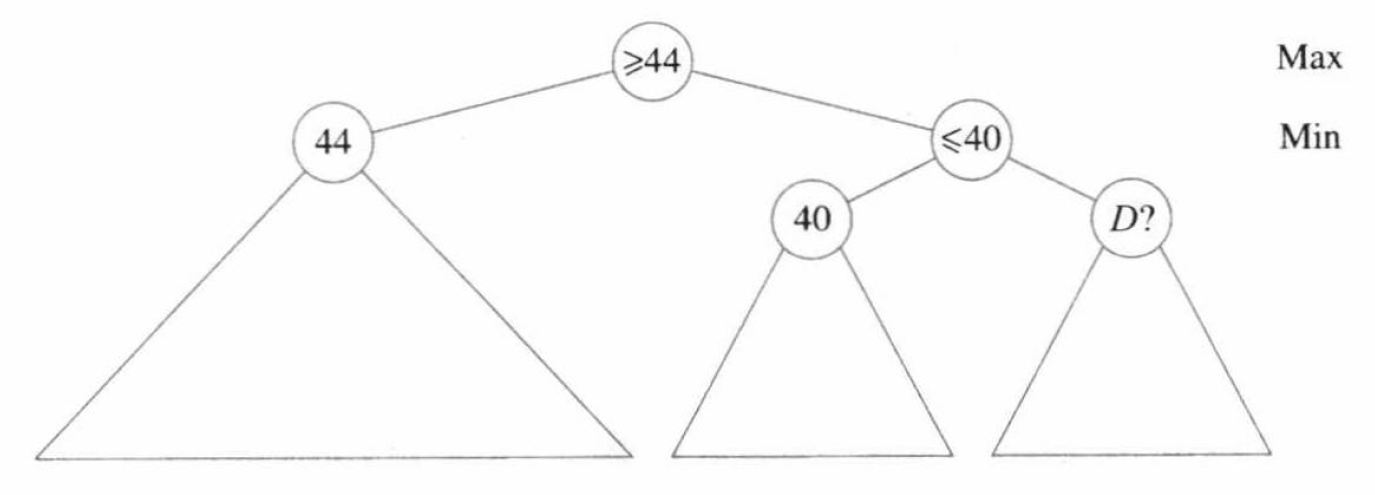
在这个决策树中，由于节点 \(D\) 的祖父节点位于 Max 层，且已经有其它分支使得其值不小于 \(44\)；节点 \(D\) 的父节点位于 Min 层，且已经有其他分支使得其值不大于 \(40\)（自然一定不大于 \(44\)）。因此无论节点 \(D\) 的值是什么，都不会影响其祖父节点，也就是决策树根的值。故对 \(D\) 节点分支的所有搜索都是不必要的。这便称作 \(\alpha\) 剪枝。

可以发现，这一剪枝符合我们上述的三个要求，首先其不影响算法的正确性，其次其理论上可以帮我们减少一半左右的搜索量，最后这一评估是容易的，只需要比较几个值就可以确定是否要进行剪枝。

\(\beta\) 剪枝就是 \(\alpha\) 剪枝的对称情况，如下例：

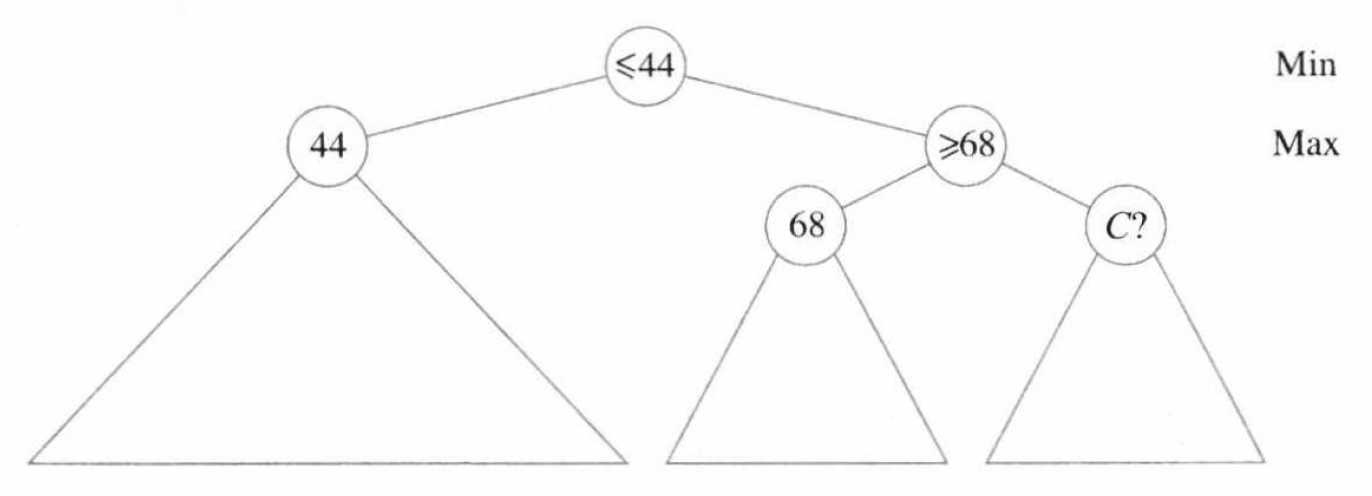
读者可以自行分析理解，为什么 \(D\) 节点分支的搜索时不必要的。