第五章 - 分治算法

约 490 个字预计阅读时间 2 分钟

用于设计算法的一种常用技巧是分治 (divide and conquer) 算法，正如这一算法的名字，其由两部分组成：

分 (divide)：递归结局较小的问题；
治 (conquer)：从子问题的解构建原问题的解。

主定理

我们先介绍分治算法的时间复杂度的分析方法。其中最重要的定理是主定理 (master theorem)。具体来说，当时间复杂度的递推关系式如下时：

\[T(N) = a T(\frac{N}{b}) + f(N), a \geq 1, b > 1\]

有

\[T(N) = \begin{cases} \Theta(N^{\log_{b}a}), & f(N) = O(N^{\log_{b}(a)-\epsilon}), \epsilon > 0 \\ \Theta(f(N)), & f(N) = \Omega(N^{\log_{b}(a) + \epsilon}), \epsilon \ge 0 \\ \Theta(N^{\log_{b}a}\log^{k + 1} N), & f(N) = \Theta(N^{\log_{b}a}\log^{k} N), k \ge 0 \end{cases}\]

需要注意的是，这里的第二种情况还需要满足正则条件 (regularity condition), 即当 \(c < 1\) 时，对于充分大的 \(N\)，有 \(a f(\frac{N}{b}) \leq c f(N)\)。

主定理的证明可以见 OI Wiki 上的介绍，证明思路是将规模为 \(N\) 的问题，分解为 \(a\) 个规模为 \(\frac{N}{b}\) 的问题，然后依次合并，直到合并到最高层。每一次合并子问题，都需要花费 \(f(N)\) 的时间。

主定理有一个重要的推论，方便我们考察何时算法复杂度可以优化到线性：

如果 \(\sum_{i = 1}^{k} \alpha_{i} < 1\)，则方程 \(T(N) = \sum_{i = 1}^{k} T(\alpha_{i} N) + O(N)\) 的解是 \(T(N) = O(N)\)。

最近点问题

接下来我们介绍一个用分治算法解决的问题，即最近点问题。具体来说，这个问题给出平面上若干点的坐标，并希望找到其中欧氏距离最小的一对点。

如果存在 \(N\) 个点，那么就存在 \(\frac{N (N - 1)}{2}\) 组点对。一个简单的想法是计算出所有点对的距离，这个做法的时间复杂度显然是 \(O(N^{2})\) 的。

接下来我们介绍一个更高效的方法。我们先将所有点按照 \(x\) 坐标排序，然后作一条直线 \(x = \frac{x_{\max} - x_{\min}}{2}\)，将点分为 \(P_{L}\) 和 \(P_{R}\) 两个部分。于是此时我们考察 3 种最近点对，分别是：

两个点都在 \(P_{L}\)，记这个最小距离为 \(d_{L}\)；
两个点都在 \(P_{R}\)，记这个最小距离为 \(d_{R}\)；
两个点一个在 \(P_{L}\)，另一个在 \(P_{R}\)，记这个最小距离为 \(d_{C}\)。

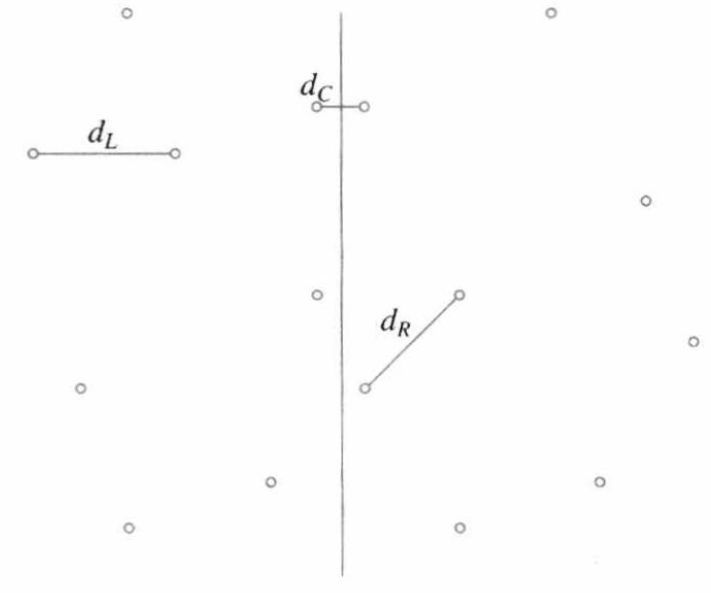
此时最终的答案就是 \(d_{L}, d_{R}, d_{C}\) 中的最小值。

显然 \(d_{L}\) 和 \(d_{R}\) 将通过对 \(P_{L}\) 和 \(P_{R}\) 递归处理得到，我们的核心就在于高效地求得 \(d_{C}\)。令 \(\delta = \min {d_{L}, d_{R}}\)，如果 \(d_{C}\) 对 \(\delta\) 有所改进，那么距离为 \(d_{C}\) 的这个点对就必然位于区域 \(x \in U(\frac{x_{\max} - x_{\min}}{2}, \delta)\) 之中，我们将这个区域称作一条带 (strip)。

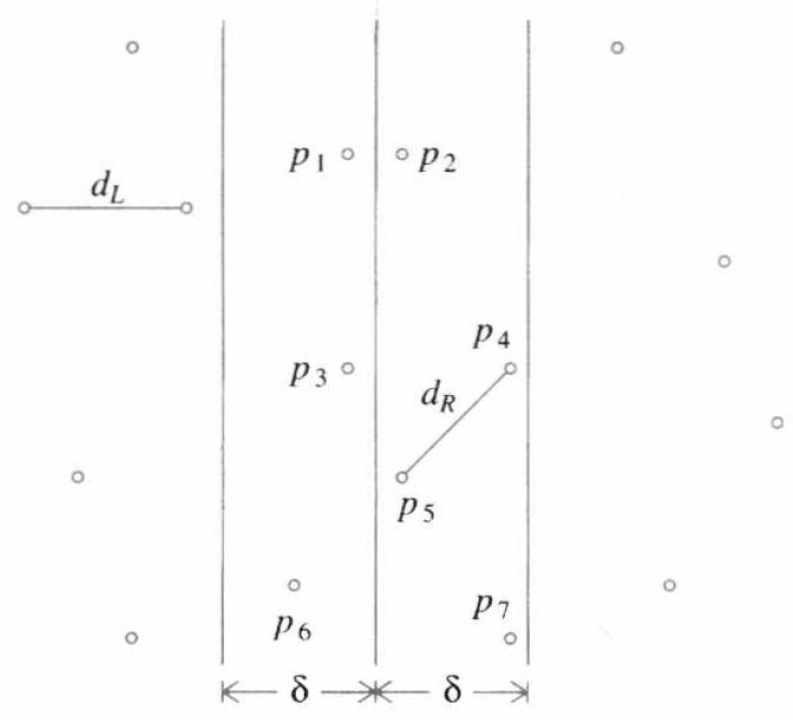
进一步地，距离为 \(d_{C}\) 的这个点对的 \(y\) 坐标差值也应当不大于 \(\delta\)。于是我们对这个带中的所有点按 \(y\) 坐标再排序，然后，每次只考察一个 \(\delta \times 2 \delta\) 的区域。由于每个这样的区域中的点的个数是 \(O(1)\) 的，于是我们就可以在 \(O(N)\) 的时间内求出 \(d_{C}\)。

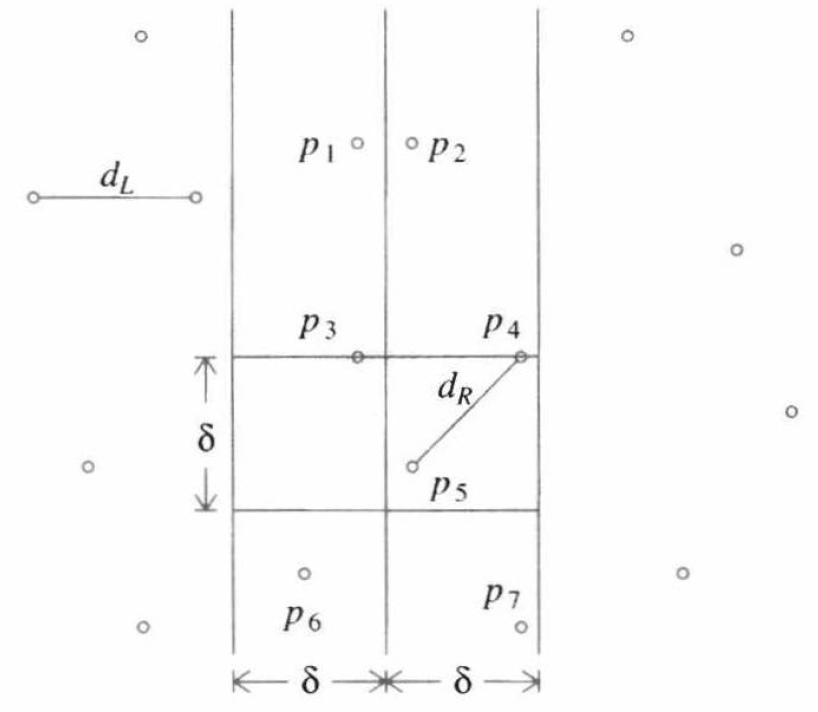
最后，我们将时间复杂度写作递推式 \(T(N) = 2 T(\frac{N}{2}) + O(N)\)，应用主定理解得 \(T(N) = O(N \log N)\)。这是一个更优的算法。