第三章 - 计算机的算术运算

约 3586 个字预计阅读时间 12 分钟

加法和减法

二进制的加法和减法是简单的，需要了解的是如何判断溢出 (overflow)。

对于有符号数在补码下的运算，我们可以得到这样的溢出条件：

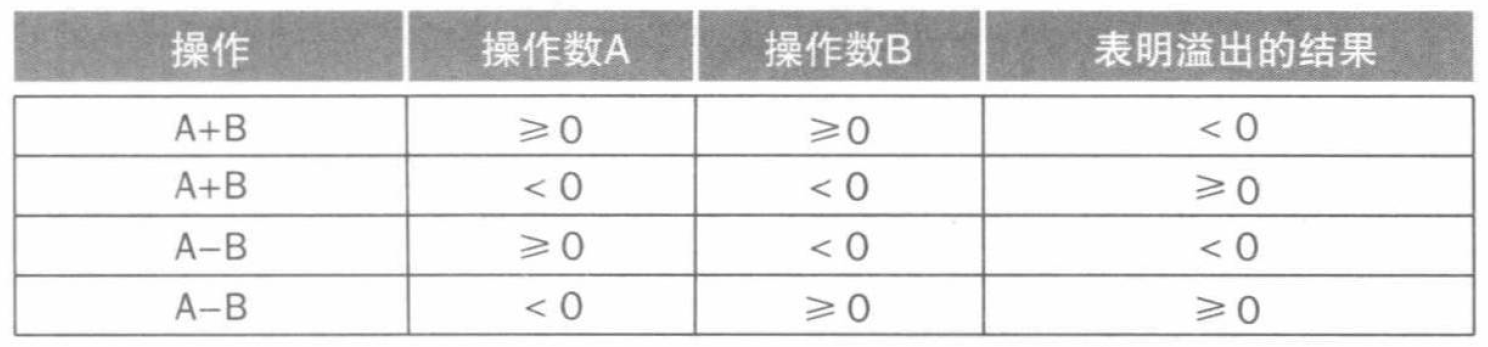
而对于无符号数，我们则将溢出视作进位或借位后的正常结果，所以一般忽略而无需进一步的操作。

能够实现加法和减法运算的硬件称作算术逻辑单元 (Arithmetic Logic Unit, ALU)。接下来我们来构造这一硬件。

1 位 ALU

1 位 ALU 的和与或运算是容易实现的，只需要引入对应逻辑门即可。而加法运算则需要 1 位全加器实现，减法运算只需要在执行加法运算前取补码。

于是将这三部分组合在一起即可实现 1 位 ALU。

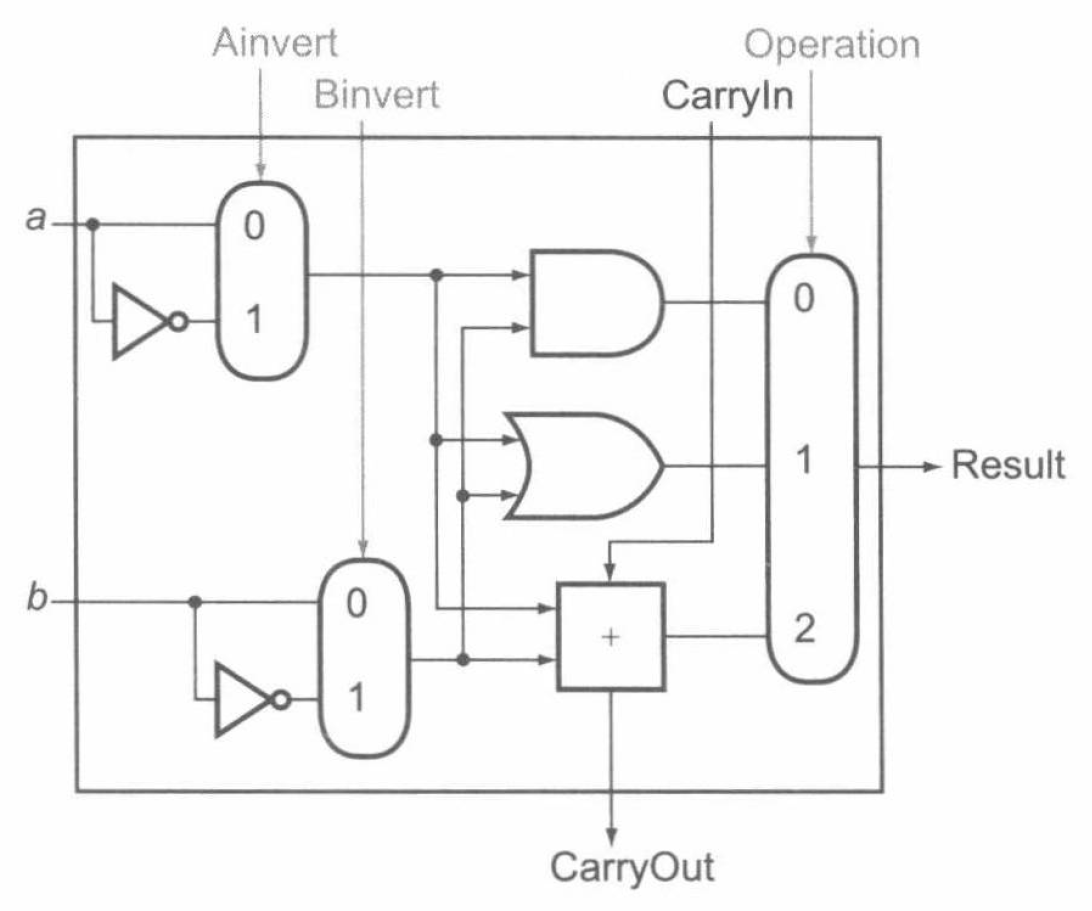
64 位 ALU

类似于行波进位加法器，我们只需要将 64 个 1 位 ALU 相连，即可得到 64 位 ALU。

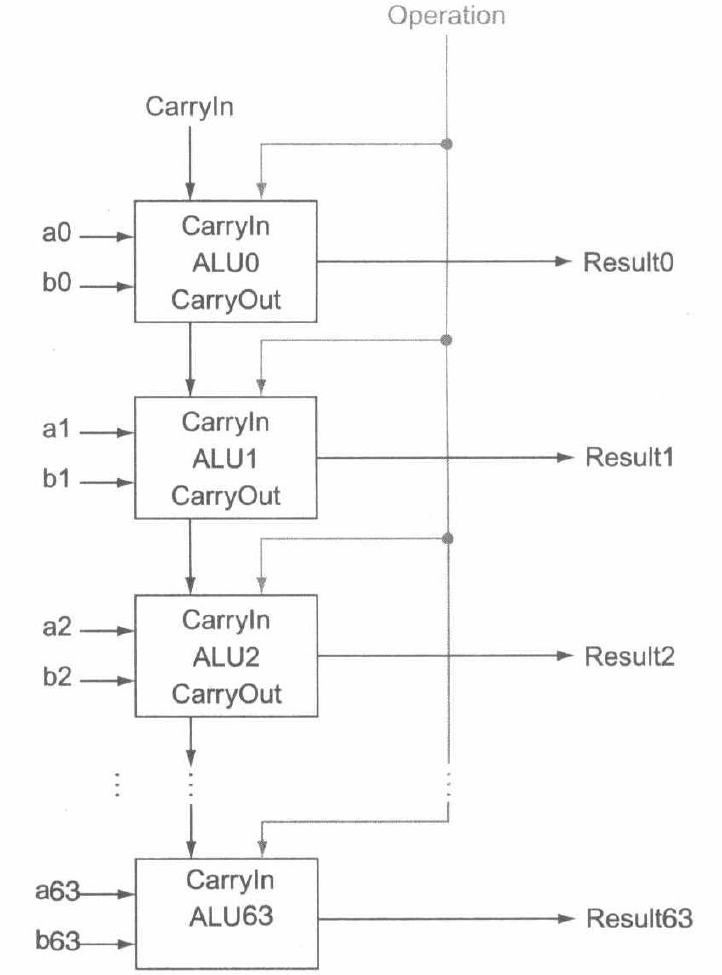
修改 64 位 ALU 以适应 RISC-V

目前设计的 ALU 已经支持加、减、与、或四种操作，而且实际上也顺带实现了其他一些逻辑操作。作为逻辑电路其功能已经足够了，但在实际的指令集中这一设计还不完整。

还需支持的一条指令是小于置位指令 slt。如果 \(rs1 < rs2\)，则操作产生 \(1\)，否则返回 \(0\)。为实现这一点，首先需要为 ALU 添加一个输入 Less。此时，只需将除最低位外的 Less 均置 \(0\)，并将减法运算结果的最高位（符号位，即图中的 Set）连接到最低位的 Less 即可。此时得到的 1 位 ALU 如下图：

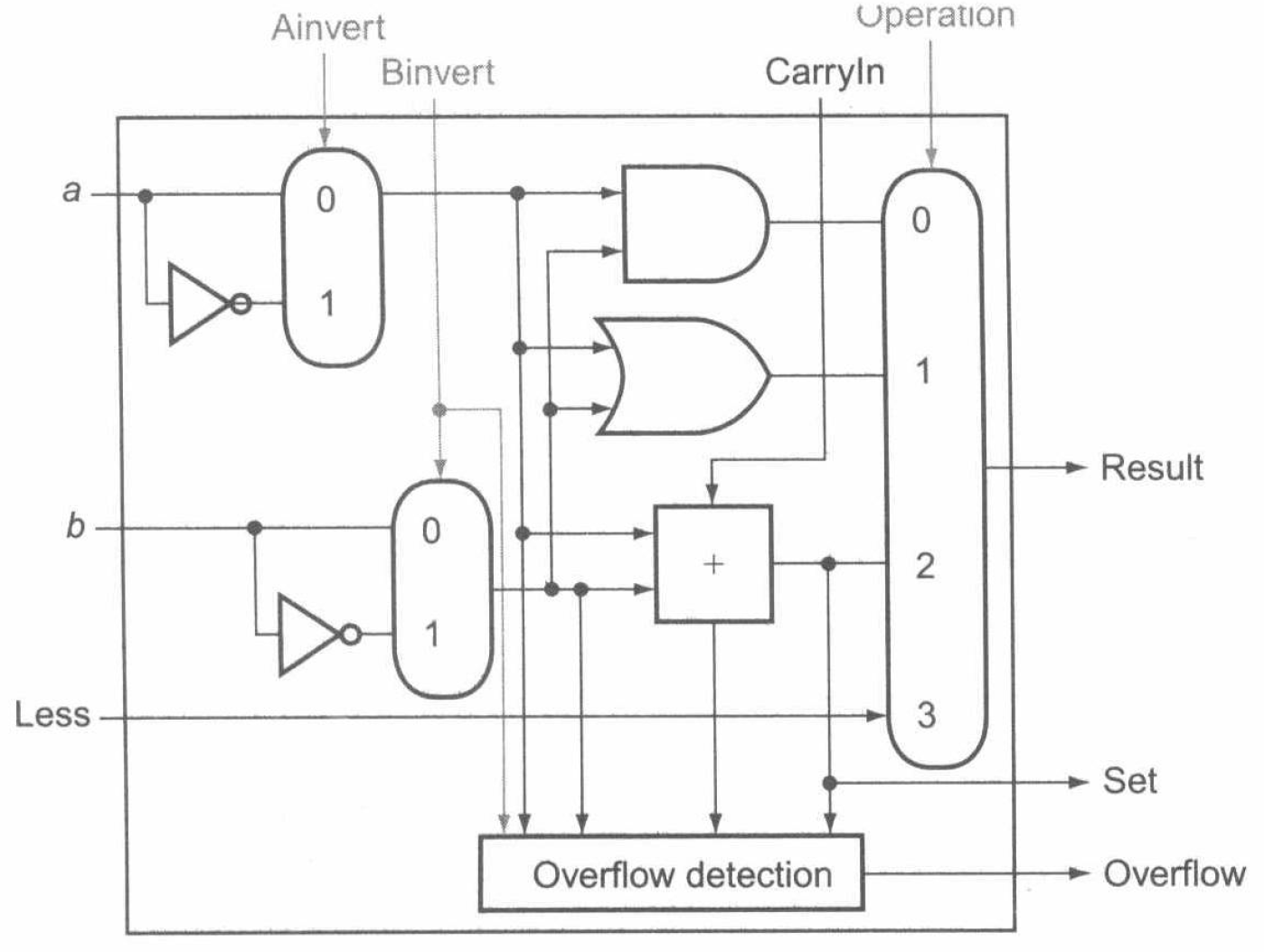
此外，ALU 还需要能够进行相等判断，以支持条件分支指令。这一操作也是简单的，只需判断减法运算的结果是否为 \(0\)。

同时，由于每次使用 ALU 做减法时，要将 CarryIn 和 Binvert 都设置为 \(1\)，其余时候都设置为 \(0\)。因此也常将这两条控制线合成为一条控制线 Bnegate。于是最终的完整 ALU 如下：

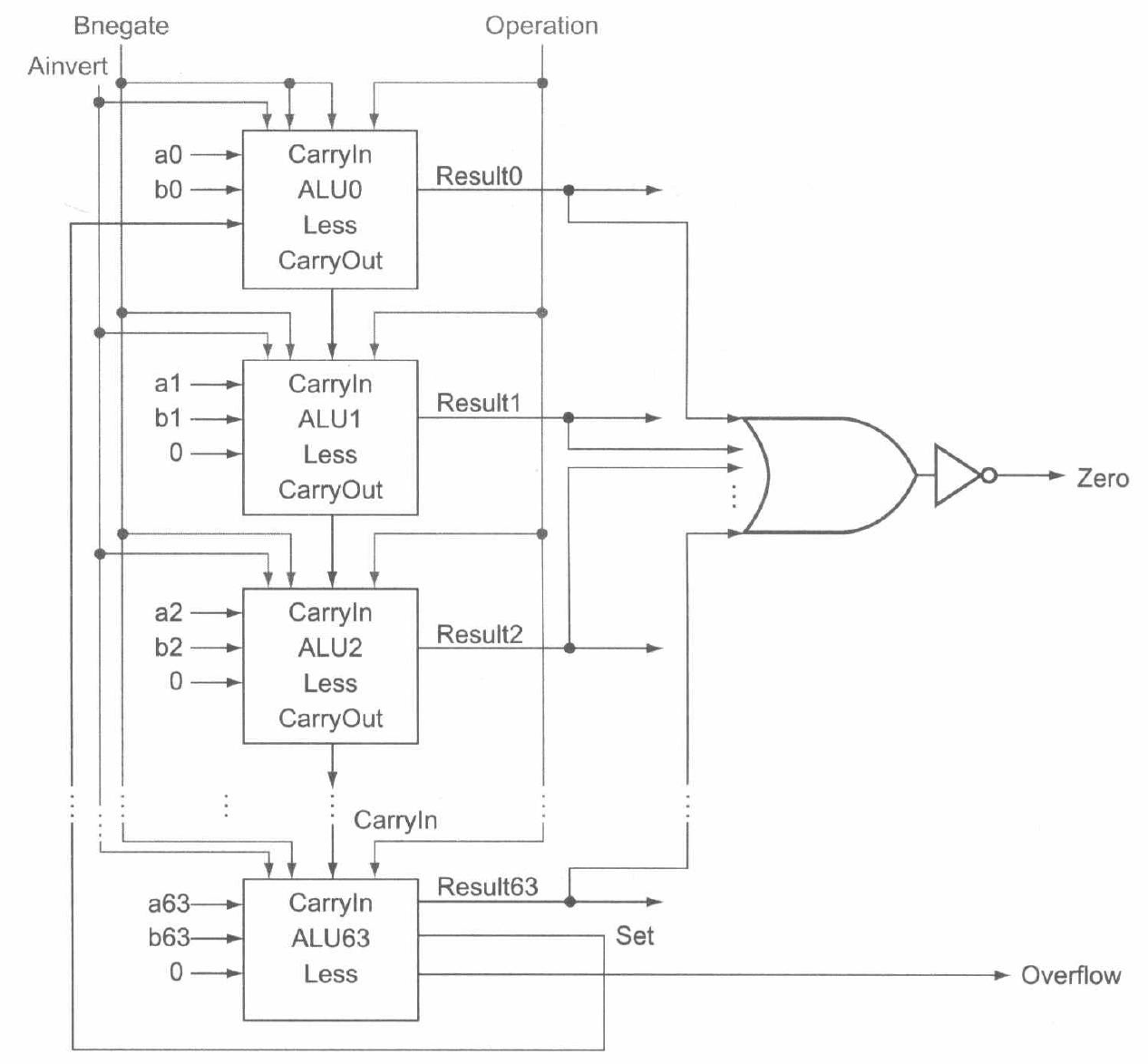
其控制线输入和对应的功能为：

Ainvert	Bnegate	Operation	功能
`0`	`0`	`00`	与
`0`	`0`	`01`	或
`0`	`0`	`10`	加
`0`	`0`	`11`	减
`0`	`1`	`11`	小于比较复位
`1`	`1`	`00`	或非

最后我们通常用如下的记号表示 ALU：

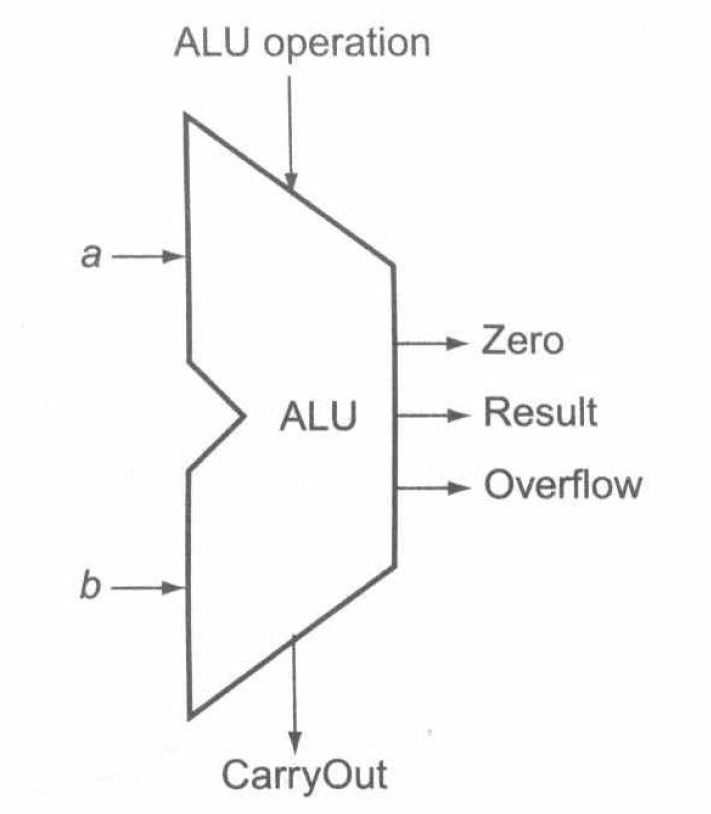
超前进位

前面我们提到，行波进位是一种直观的实现方式度是不尽人意的。对应的一种机制，即超前进位加法器 (vary-lookahead adder) 就是用于解决这一问题。

我们记每一位的两个输入为 \(a_{i}\) 和 \(b_{i}\)，进位为 \(\text{CarryIn}_{i}\)，简记为 \(c_{i}\)。于是通过简单的变形我们可以得到

\[c_{i + 1} = a_{i} b_{i} + a_{i} c_{i} + b_{i} c_{i} = a_{i} b_{i} + (a_{i} + b_{i}) c_{i}\]

于是我们记 \(g_{i} = a_{i} b_{i}\)，称作生成因子 (generate factor)；\(p_{i} = a_{i} + b_{i}\)，称作传播因子 (propagate)。从而得到

\[c_{i + 1} = g_{i} + p_{i} c_{i}\]

于是利用此进行第一级抽象，可以更简洁地计算进位。4 位的进位如下：

\[\begin{aligned} c_{1} & = g_{0} + p_{0} c_{0} \\ c_{2} & = g_{1} + p_{1} g_{0} + p_{1} p_{0} c_{0} \\ c_{3} & = g_{2} + p_{2} g_{1} + p_{2} p_{1} g_{0} + p_{2} p_{1} p_{0} c_{0} \\ c_{4} & = g_{3} + p_{3} g_{2} + p_{3} p_{2} g_{1} + p_{3} p_{2} p_{1} g_{0} + p_{3} p_{2} p_{1} p_{0} c_{0} \end{aligned}\]

但是这种形式虽然避免了行波的等待时间，但是表达式仍然冗长，于是我们要进行两级抽象。

例如，当我们用四个 4 位加法器组成 16 位加法器时，我们用 \(P_{i}\) 表示整个子加法器的传播信号，仅当其中每一位都传播进位时才为真。

\[\begin{aligned} P_{0} & = p_{3} p_{2} p_{1} p_{0} \\ P_{1} & = p_{7} p_{6} p_{5} p_{4} \\ P_{2} & = p_{11} p_{10} p_{9} p_{8} \\ P_{3} & = p_{15} p_{14} p_{13} p_{12} \end{aligned}\]

类似地，我们用 \(G_{i}\) 表示整个子加法器的传播信号，仅当其最高有效位生成进位时才为真。

\[\begin{aligned} G_{0} & = g_{3} + p_{3} g_{2} + p_{3} p_{2} g_{1} + p_{3} p_{2} p_{1} g_{0} \\ G_{1} & = g_{7} + p_{7} g_{6} + p_{7} p_{6} g_{5} + p_{7} p_{6} p_{5} g_{4} \\ G_{2} & = g_{11} + p_{11} g_{10} + p_{11} p_{10} g_{9} + p_{11} p_{10} p_{9} g_{8} \\ G_{3} & = g_{15} + p_{15} g_{14} + p_{15} p_{14} g_{13} + p_{15} p_{14} p_{13} g_{12} \end{aligned}\]

于是基于第二级的传播和生成因子，我们可以得到每个子加法器的进位信号表示：

\[\begin{aligned} C_{1} & = G_{0} + P_{0} c_{0} \\ C_{2} & = G_{1} + P_{1} G_{0} + P_{1} P_{0} c_{0} \\ C_{3} & = G_{2} + P_{2} G_{1} + P_{2} P_{1} G_{0} + P_{2} P_{1} P_{0} c_{0} \\ C_{4} & = G_{3} + P_{3} G_{2} + P_{3} P_{2} G_{1} + P_{3} P_{2} P_{1} G_{0} + P_{3} P_{2} P_{1} P_{0} c_{0} \end{aligned}\]

据此，我们可以设计出 16 位的超前进位加法器：

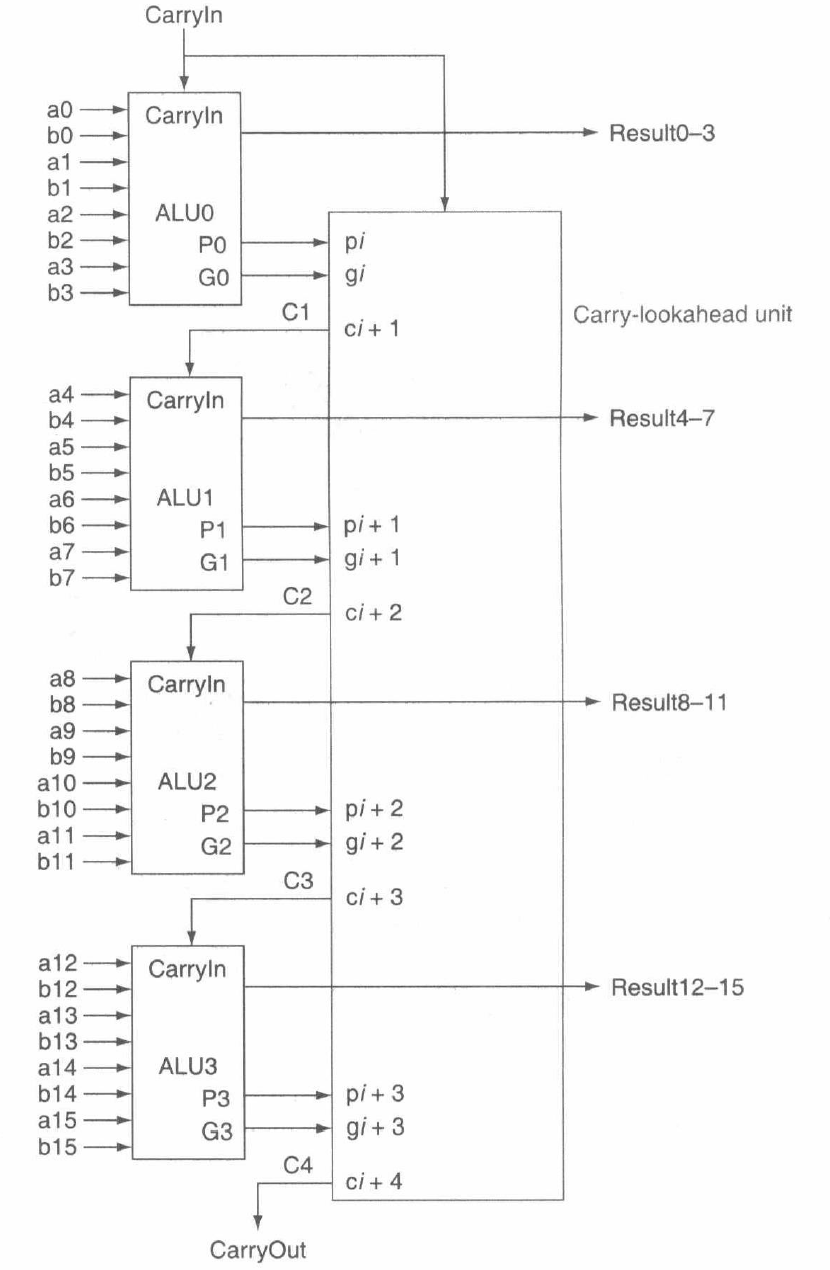
此时，我们可以对超前进位和行波进位加法器的速度做一个对比。以计算 \(c_{15}\)（即 \(C_{4}\)）的门延迟数为例，行波进位的每一位进位需要两个门延迟，于是门延迟数是 \(16 \times 2 = 32\)；而超前进位中 \(p_{i}, g_{i}\) 都是由 \(a_{i}, b_{i}\) 定义的一级逻辑，在两级抽象下仅需 \(2 + 2 + 1 = 5\) 个门延迟。因此在 16 位加法器中超前进位比行波进位快 6 倍，这一优势会在更大规模的加法器中会更显著。

乘法

串行乘法

二进制乘法的实现思路是容易的。只需要将被乘数不断左移，并在乘数位是 \(1\) 时将左移后的被乘数加到结果上即可。据此实现的 64 位乘法器如下：

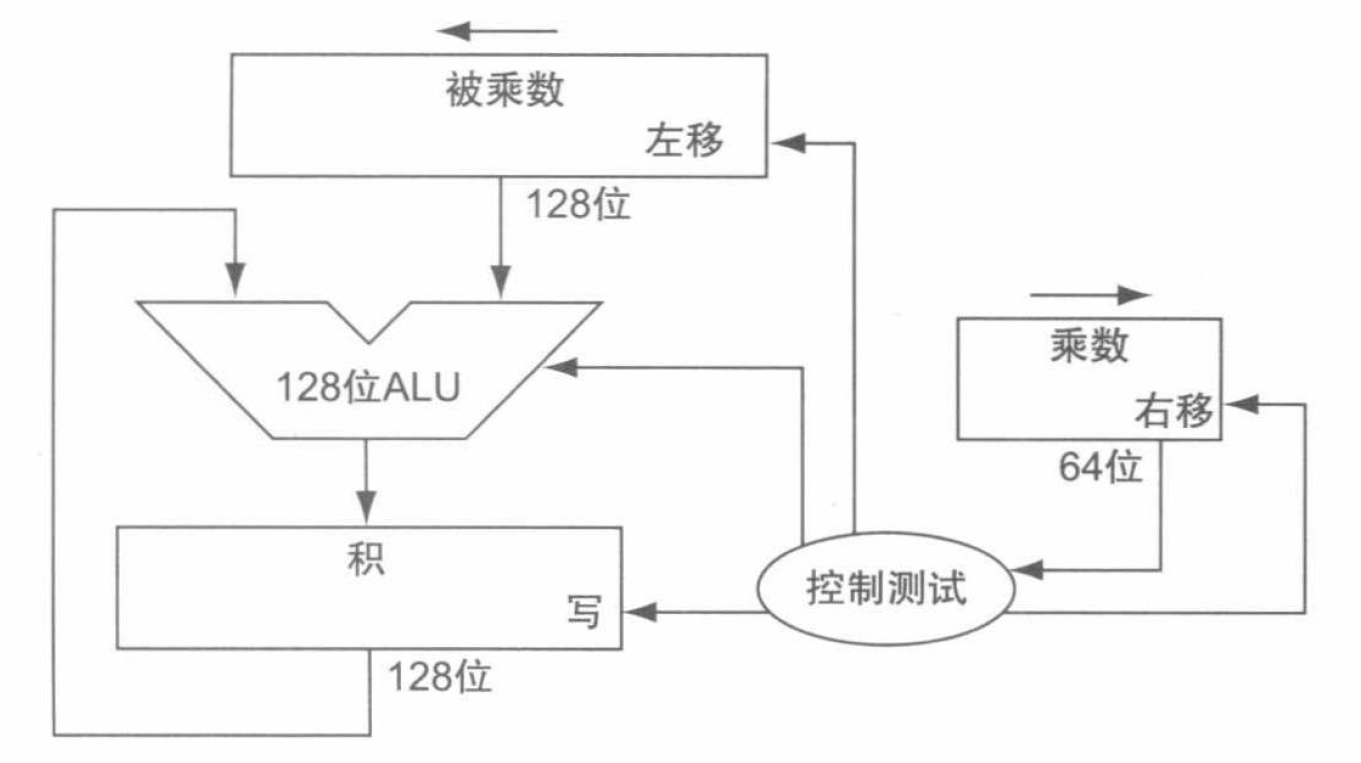
但是根据这个朴素的思路设计出的乘法器存在一些问题。为了计算 64 位的乘数和被乘数的乘法，需要我们使用一个 128 位的 ALU 辅助我们完成中间的运算。于是在注意到寄存器和加法器有未使用的部分后，我们可以高效地利用积寄存器，将乘数放到积寄存器的右半部分。如果乘数的最右位是 \(1\)，那么对被乘数和乘数进行移位，并同时将被乘数加到积上。据此我们可以得到改进后的乘法器：

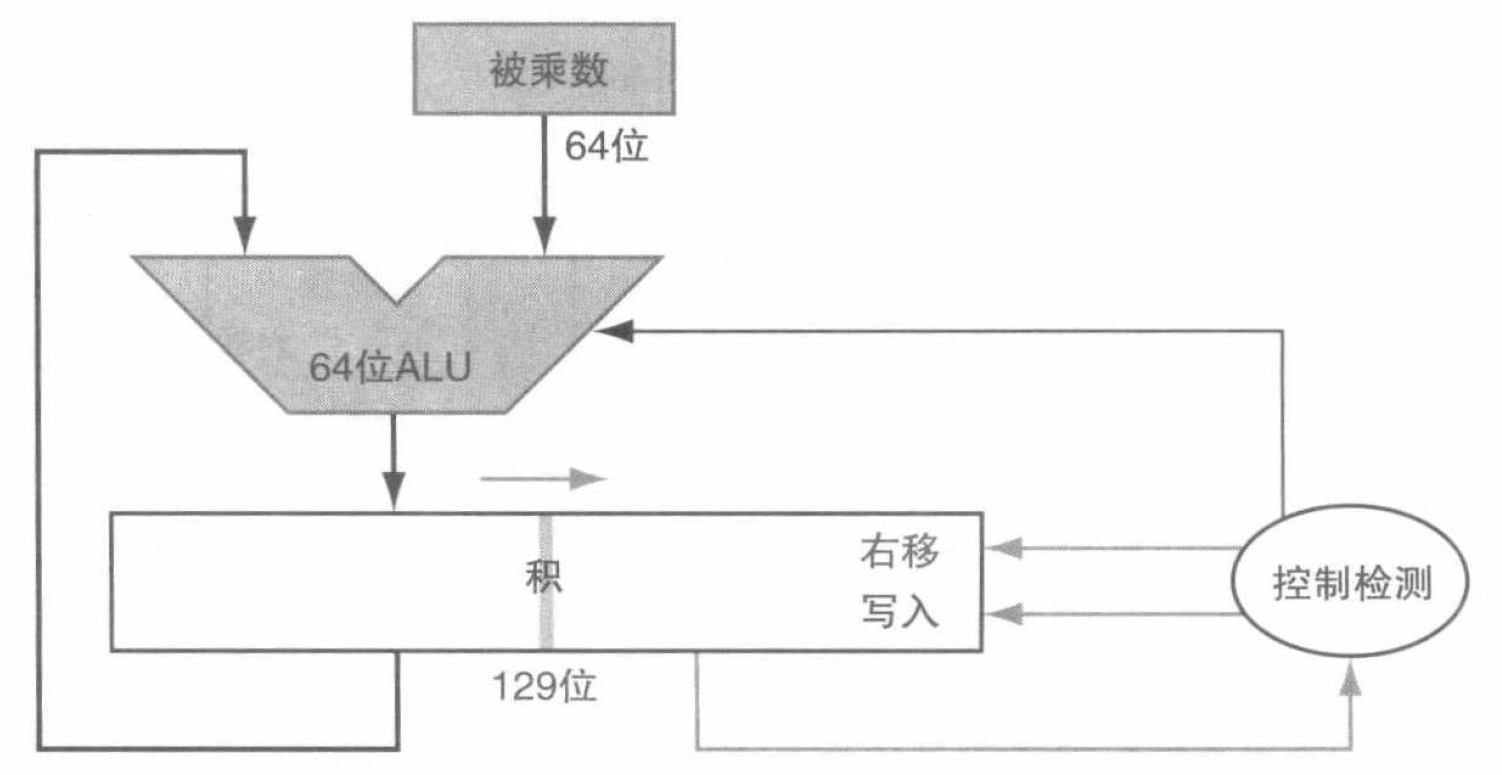
带符号乘法的处理是容易的，只需要单独根据符号位确定积的符号位，并取被乘数和乘数的绝对值相乘即可。

快速乘法

通过在乘法运算开始时检查 64 个乘数位，就可以判定是否要将被乘数加上。快速惩罚可以通过为每个乘数位提供一个 64 位加法器来实现，每个加法器计算被乘数和乘数位相与的结果和上一个加法器的输出之和。

但显然，通过简单地将低位加法器的输出端连接到高位加法器的输入端来组织这 64 个加法器，仍然需要 64 次 64 位加法的时间来完成运算。更明智的方法是将其组织成如下图的并行树，于是我们只需要 \(\log_{2} 64\) 次 64 位加法的时间就能完成运算。

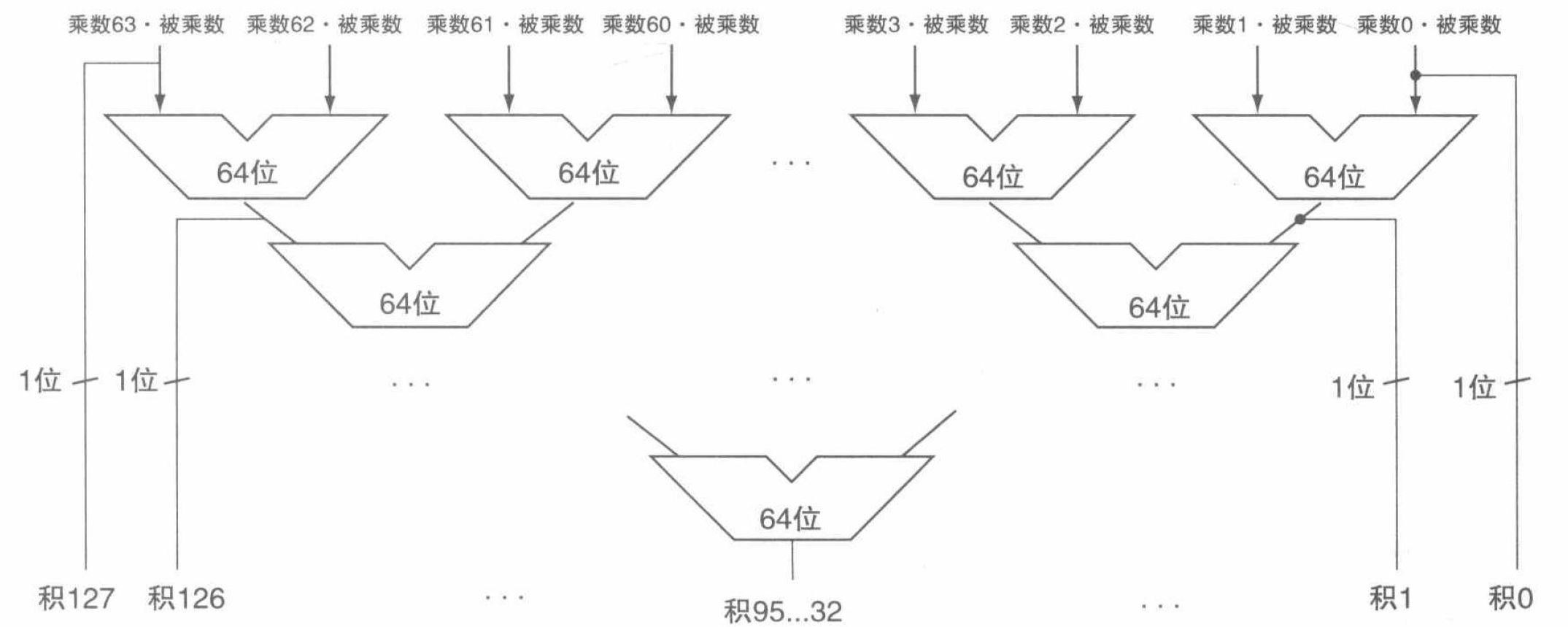
RISC-V 中的乘法

mul rd, rs1, rs2：64 位乘法，rd 保存 128 位乘积的低 64 位
mulh rd, rs1, rs2：64 位乘法，rd 保存 128 位有符号数之间的乘积的高 64 位
mulhu rd, rs1, rs2：64 位乘法，rd 保存 128 位无符号数之间的乘积的高 64 位
mulhsu rd, rs1, rs2：64 位乘法，rd 保存 128 位无符号数和有符号数的乘积的高 64 位

除法

串行除法

除法的实现和乘法类似，我们直接给出改进过的 64 位除法器：

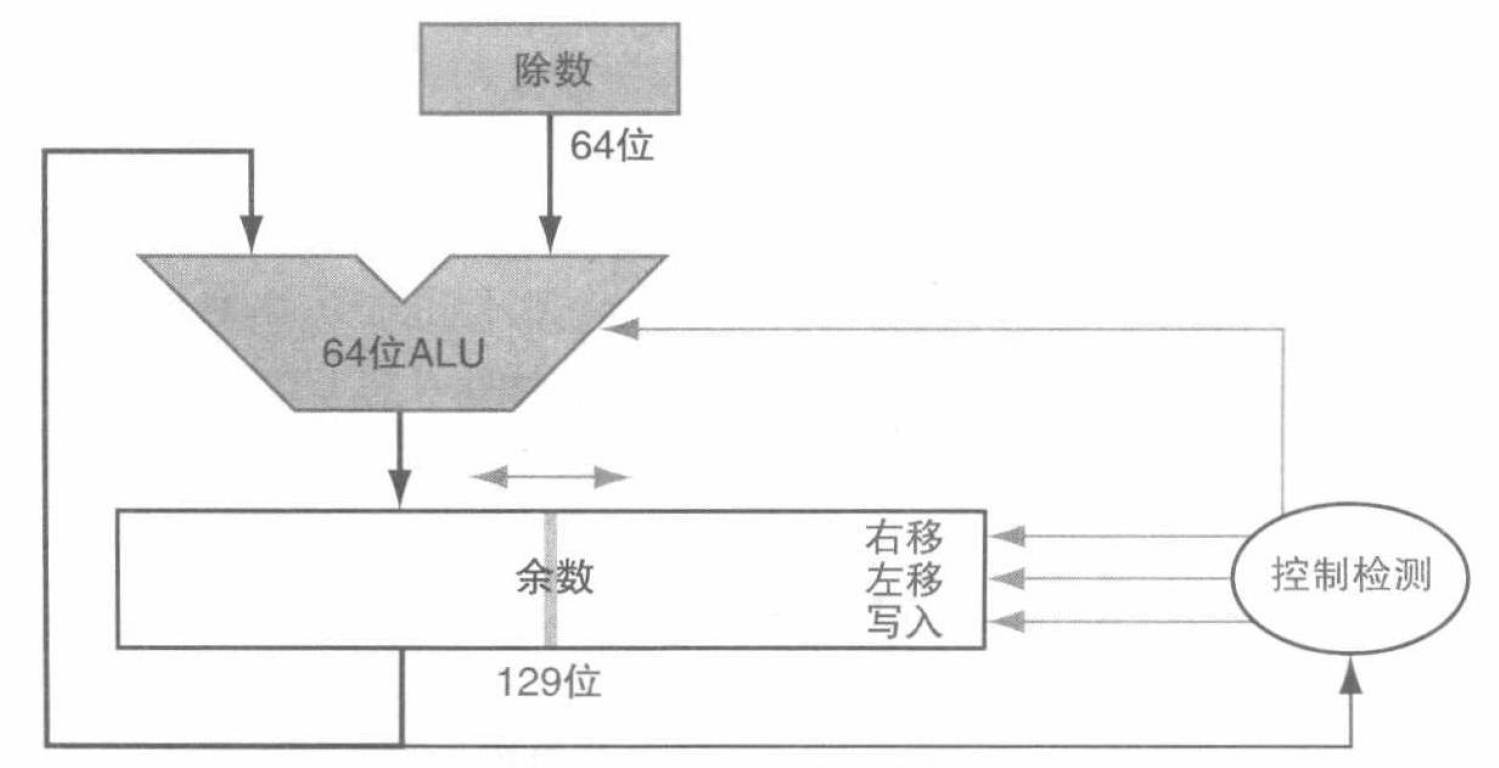
即我们首先把被除数放到余数寄存器的低 64 位。之后每次从余数寄存器的高 64 位中减去除数寄存器，并检查余数。如果余数非负，则把结果放入余数寄存器的高 64 位，并左移商寄存器后将新的最低位设置为 \(1\)。否则不更新余数寄存器，直接左移商寄存器并将新的最低位设置为 \(0\)。再右移除数寄存器并重复以上操作。最后余数即存放在余数寄存器的高 64 位，商存放在余数寄存器的低 64 位。

改进后的除数寄存器把商寄存器和余数寄存器右半部分拼接，从而只需要 64 位 ALU 辅助运算。

带符号除法

带符号除法的处理是容易的，只需要单独根据符号位确定商的符号位，并取被除数数和除数的绝对值相除即可。

但容易指导，可能有多组商和余数满足其与被除数和除数的代数关系。因此我们需要设定一组规则来决定余数的值，即：

余数的符号位与被除数的符号位相同
余数的绝对值小于除数的绝对值

快速除法

除法不能用类似于乘法的方法简单地进行并行加速，因为中间过程会产生很多减法运算，余数寄存器上的符号位是随时变化的，且依赖于运算的顺序。

所以一个改进措施称作SRT 除法 (SRT division)，其根据被除数和余数的高位来查找表，以预测除法中每步的可能的商，并通过后续步骤纠正错误的预测。当下的典型算法中采用的是余数的 6 位和除数的 4 位来索引查找表。这种快速方法的准确性取决于查找表中的值是否合适。

RISC-V 中的除法

div rd, rs1, rs2：rd 保存有符号数除法的商
divu rd, rs1, rs2：rd 保存无符号数除法的商
rem rd, rs1, rs2：rd 保存有符号数除法的余数
remu rd, rs1, rs2：rd 保存无符号数除法的余数

浮点运算

浮点表示

通常来说，浮点数可以这样表示：

\[(-1)^{S} \times F \times 2^{E}\]

即包括符号 \(S\)、指数 (exponent) \(E\) 和尾数 (fraction) \(F\) 三部分。同时我们要求这一表示应当符合规格化 (normalised) 的科学计数法，即尾数的整数部分只能有一位数字且不为 \(0\)。

于是在计算机中，决定浮点数表示精确性的关键在于分配给指数和尾数的位数。据此我们得到两种标准：

单精度 (float)：\(2.0_{10} \times 10^{-38} \sim 2.0_{10} \times 10^{38}\)

双精度 (double)：\(2.0_{10} \times 10^{-308} \sim 2.0_{10} \times 10^{308}\)

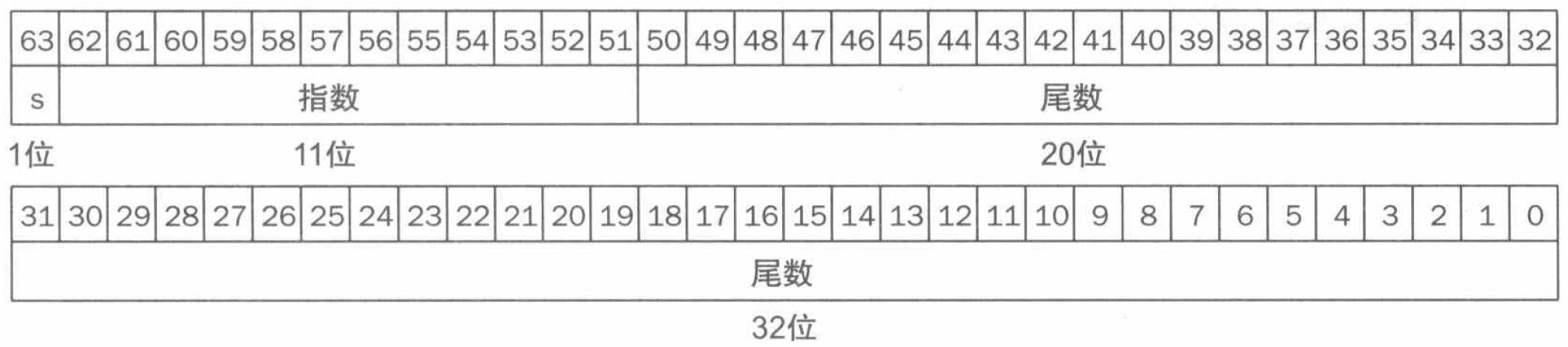
当然，我们也会关注这种表示方法下数的精度。根据两种标准下尾数的位数以及二进制和十进制的换算，可以知道单精度数的精度约为 6 位十进制数，双精度数的精度约为 16 位十进制数。

进一步地，由于二进制下的非零规范化数的整数部分一定是 \(1\)，因此为了存储更多的数字，我们就省去这一前导位，并将这一位的空间用于表示尾数，因此实际单精度浮点数的尾数为 24 位，双精度浮点数的尾数为 53 位。实际上用于表示浮点数的尾数位被称作有效位数 (significand)。于是我们可以这么表示一个浮点数：

\[(-1)^{S} \times (1 + \text{尾数}) \times 2^{E}\]

其中尾数位表示大小在 \(0\) 到 \(1\) 之间的小数，如果将尾数的各位从左到右依次用 \(s_{1}, s_{2}, s_{3}, \cdots\) 表示，那数的值为：

\[(-1)^{S} \times (1 + (s_{1} \times 2^{-1}) + (s_{2} \times 2^{-2}) + (s_{3} \times 2^{-3}) + \cdots) \times 2^{E}\]

按照符号、指数、尾数的顺序存储浮点数，有助于进行浮点数的比较：先比较符号位，再比较指数，最后比较尾数。但正数和负数之间的比较就比较麻烦了：如果用补码表示指数位，那么负指数反而会显得比较大。

因此，最理想的表示法是将最小的负指数表示为 \(00 \cdots 00_{2}\)，最大的正指数表示为 \(11 \cdots 11_{2}\)，这样就可以直接做无符号数的比较，便于计算机处理。这种表示法称作移码表示法(biased notation)。

根据定义容易得到，单精度浮点数的偏移值为 \(127\)，双精度浮点数的偏移值为 \(1023\)。带偏移值的指数意味着一个由浮点数表示的值实际上是：

\[(-1)^{S} \times (1 + \text{有效位数}) \times 2^{\text{指数} - \text{偏移值}}\]

浮点加法

浮点数加法的步骤可以归结为：

将较小数的有效数位进行右移，直到其指数和较大数的指数一致，使得两个数的小数点对齐；
将两个数的有效数位相加；
对和进行移位以调整指数大小，使得数变为规格化的形式（此时需要检测可能的上溢和下溢）；
根据有效位数对结果进行舍入。

浮点乘法

浮点数乘法的步骤可以归结为：

将操作数的指数相加得到积的指数；
将两个数的有效数位相乘；
对积进行移位以调整指数大小，使得数变为规格化的形式（此时需要检测可能的上溢和下溢）；
根据有效位数对结果进行舍入；
根据原始操作数的符号确定积的符号。

精确算术

由于在浮点数运算中会出现舍入，为了保护最终结果的精确性，我们在中间计算时总是在右边保留两个额外的位，从左到右依次为保护位 (guard) 和舍入位 (round)。

在某些情况下，我们还会保留舍入位的再右边一位，称作粘滞位 (sticky)。其取值取决于在中间运算中，舍入位右边是否有非零位。有非零位则将粘滞位设为 \(1\)，反之为 \(0\)。这有利于让计算机在运算时处理 \(0.50 \cdots 00\) 和 \(0.50 \cdots 01\) 的舍入差异，前者舍去，后者进位。