第六章 - 图论算法
约 6569 个字 179 行代码 预计阅读时间 24 分钟
概念
图的定义
一个图 (graph) \(G = (V, E)\) 由顶点 (vertex) 集 \(V\) 和边 (edge) 集 \(E\) 组成。每一条边是一个点对 \((u, v)\),有时边也称作弧 (arc)。如果点对是有序的,那么图就是有向 (directed) 的,图称作有向图 (diagraph)。有向图上去掉每条边的方向性而得到的无向图称作该有向图的基础图 (underlying graph)。顶点 \(v\) 和 \(w\) 邻接 (adjacent) 当且仅当 \((v, w) \in E\)。有时边具有权 (weight) 或值 (cost)。
图中的一条路径 (path) 是一个顶点序列 \(w_{1}, w_{2}, \cdots, w_{N}\) 满足 \((w_{i}, w_{i + 1}) \in E, 1 \leq i < N\)。一条简单路径 (simple path) 即为一条路径上各顶点互异,但第一个顶点和最后一个顶点可能相同的路径。
Note
如果图含有一条从一个顶点到它自身的边 \((v, v)\),那么路径 \(v, v\) 称作一个环 (loop)。后文我们要讨论的图都是无环的。
有向图中的圈 (cycle) 是满足 \(w_{1} = w_{N}\) 且长至少为 \(1\) 的一条路径。如果该路径是简单路径,那么这个圈就是简单圈。如果一个有向图没有圈,则称这个图是无圈的 (acyclic),这个图称作有向无圈图 (directed acyclic graph, DAG)。
如果在一个无向图中从每一个顶点到每个其它顶点都存在一条路径,则称该无向图是连通的 (connected)。具有这样性质的有向图称作强连通的 (strongly connected)。如果一个有向图不是强连通的,但其基础图是连通的,则称该有向图是弱联通的 (weakly connected)。完全图 (complete graph) 是每一对顶点间都存在一条边的图。
Note
从以上定义不难发现,树即为一个连通无圈图。
图的表示
常用的表示图的方法有两种:邻接矩阵和邻接表。
邻接矩阵
邻接矩阵 (adjacent matrix) 表示法即使用一个二维数组来表示图。其中 A[u][v] 置为边 (u, v) 的权。在具体问题中,我们常用一个非法的极小值(如 \(0\))或极大值(如 \(\infty\))表示不存在的边。
邻接矩阵的实现和调用都非常简单,潜在的问题在于其空间需求太大,为 \(\Theta(|V|^{2})\)。如果图是稠密 (dense) 的,即 \(|E| = \Theta(|V|^{2})\),那么邻接矩阵是合适的表示方法。但如果图是稀疏 (sparse) 的,即边的数量远小于 \(|V|^{2}\),那么使用邻接矩阵的空间需求就不大可接受了。
邻接表
对于稀疏图,更好的表示方法是使用邻接表 (adjacency)。其结构示例如下:

由图可见,对每一个顶点,我们使用一个表存放所有与该顶点邻接的顶点。同时我们再用一个头单元 (header cell) 数组,即图中最左边的结构作为各顶点的索引。此时的空间需求为 \(O(|E| + |V|)\)。
拓扑排序
拓扑排序 (topological sorting) 是对有向无圈图各顶点的一种排序得到一个拓扑序列,其保证对于任何有向边 \((u, v)\),在排序得到的序列中都有 \(u\) 在 \(v\) 的前面。
为了解决这个问题,我们先再作出以下定义:称一个顶点 \(v\) 的入度 (indegree) 为以 \(v\) 为终点的边 \((u, v)\) 的条数,其出度 (outdegree) 为以 \(v\) 为起点的边 \((v, u)\) 的条数。两者之和称作顶点 \(v\) 的度 (degree)。
构造拓扑序列的算法是简单的,只需要重复以下两步:
- 从图中选择一个入度为 0 的顶点。
- 输出该顶点,从图中删除此顶点及其所有的出边。
其伪代码如下:
void Topsort(Graph G) {
int Counter;
Vertex V, W;
for (Counter = 0; Counter < NumVertex; Counter++) {
V = FindNewVertexOfIndegreeZero();
if (V == NotAVertex) {
Error("Graph has a cycle");
break;
}
TopNum[V] = Counter;
for each W adjacent to V {
Indegree[W]--;
}
}
}
不难得到,这个算法的复杂度为 \(O(|V|^{2})\)。
接下来我们着手改进这个算法。可以发现其最大的时间复杂度开销源自于寻找入度为 0 的点,每次寻找都要花费 \(O(|V|)\) 的时间,而这样的寻找有 \(|V|\) 次。但事实上,如果我们能对入度为 0 的点用一个集合进行记录,并在删除边时对这个集合进行更新,我们就能避免 \(O(|V|)\) 的寻找而达到相同的效果。
在具体的实现中,这个集合可以用栈或队列实现。我们给出用队列实现的伪代码:
void Topsort(Graph G) {
Queue Q;
int Counter = 0;
Vertex V, W;
Q = CreateQueue(NumVertex); MakeEmpty(Q);
for each vertex V {
if (Indegree[V] == 0) {
Enqueue(V, Q);
}
}
while (!IsEmpty(Q)) {
V = Dequeue(Q);
TopNum[V] = ++Counter;
for each W adjacent to V {
if (--Indegree[W] == 0) {
Enqueue(W, Q);
}
}
}
if (Counter != NumVertex) {
Error("Graph has a cycle");
}
DisposeQueue(Q);
}
当使用邻接表表示图时,这个算法的时间复杂度即为 \(O(|E| + |V|)\)。
从以上讨论中我们可以发现,拓扑排序的结果是不唯一的。如果我们希望得到字典序最小(或最大)的拓扑序列,我们只需将上述算法中存放入度为 0 的顶点的数据结构由队列换为最小堆(或最大堆)即可。
最短路径算法
对于一个赋权图,即每条边 \((v_{i}, v_{j})\) 具有边权 \(c_{i, j}\),则路径 \(v_{1} v_{2} \cdots v_{N}\) 赋权路径长 (weighted path length) 即为 \(\sum_{i = 1}^{N - 1} c_{i, i + 1}\),无权路径长 (unweighted path length) 只是路径上的边数,即 \(N - 1\)。
一般地,我们要解决单源最短路径问题,即给定一个赋权图 \(G = (V, E)\) 和一个指定顶点 \(s\) 作为输入,找出 \(s\) 到 \(G\) 中每个其他顶点的最短赋权路径。
在讨论解决这一问题的算法之前,我们需要先关注一些可能的特殊情况。
首先,对于有向图,两个节点之间不一定有路径。其次,如果一个图中存在「负权边」,即边权为负数的边,那么就要关注是否有负值圈 (negative-cost cycle),即一个总路径长为负数的循环路径。如果有负值圈存在,那么路径就可以包含循环路径任意多次,故这种情况下没有最短路径。
无权最短路径
对于无权图,每条边都是等价的,故我们只需考察起点到达每个终点的最少边数。一个简单的想法是利用广度优先搜索 (breadth-first search),即按层处理顶点。
为了做到这一点,我们需要记录一些信息。我们用 \(d_{v}\) 记录从 \(s\) 出发到达顶点 \(v\) 的路径长度。在开始时除 \(d_{s} = 0\) 外,其余顶点的 \(d_{v}\) 均为 \(\infty\)。我们用 \(p_{v}\) 记录顶点 \(v\) 第一次被访问的来源,即是从哪个前驱顶点出发的路径被访问到的。记录 \(p_{v}\) 可以得到最短路的路径。最后,我们自然需要一个 Known 来记录每个顶点是否被访问到了。当一个顶点已经被访问过了,我们就不会再去寻找到达它的更短路径了。
有了这些信息,算法的伪代码如下:
void Unweighed(Table T) {
int CurrDist;
Vertex V, W;
for (CurrDist = 0; CurrDist < NumVertex; CurrDist++) {
for each vertex V {
if (!T[V].Known && T[V].Dist == CurrDist) {
T[V].Known = True;
for each W adjacent to V {
if (T[W].Dist == Infinity) {
T[W].Dist = CurrDist + 1;
T[W].Path = V;
}
}
}
}
}
}
注意到双层嵌套的 for 循环,该算法的时间复杂度为 \(O(|V|^{2})\)。算法的低效之处在于,就算所有顶点都已经有 Known 标记了,最外层的循环仍然要继续。这一点在不修改核心算法的情况下是难以改进的。
分析代码,可以发现如果我们能记录所有 \(d_{v} = \texttt{CurrDist}\) 和 \(d_{v} = \texttt{CurrDist} + 1\) 的顶点,我们就不必每次遍历全图来寻找适于下一次访问的顶点。于是我们采用队列这一数据结构来完成记录。
在每轮迭代开始时,队列中含有距离为 \(\texttt{CurrDist}\) 的顶点。然后我们将这些顶点顺次出队,并将由它们出发访问得到的,距离为 \(\texttt{CurrDist} + 1\) 的顶点入队。当所有距离为 \(\texttt{CurrDist}\) 的顶点出队后,一轮迭代结束,此时队列里就只含有距离为 \(\texttt{CurrDist} + 1\) 的顶点,即为下一轮迭代的初始条件。
容易想到,按照这样的迭代方法,如果一个顶点到最后距离仍然为 \(\infty\),则表明其是从开始结点出发不可达的。于是我们便不再需要 Known 标记。改进后的伪代码如下:
void Unweighted(Table T) {
Queue Q;
Vertex V, W;
Q = CreateQueue(NumVertex); MakeEmpty(Q);
Enqueue(S, Q);
while (!IsEmpty(Q)) {
V = Dequeue(Q);
for each W adjacent to V {
if (T[W].Dist == Infinity) {
T[W].Dist = T[V].Dist + 1;
T[W].Path = V;
Enqueue(W, Q);
}
}
}
DisposeQueue(Q);
}
使用邻接表储存图的话,该算法的时间复杂度即为 \(O(|E| + |V|)\)。
Dijkstra 算法
对于赋权图,处理方法就有所不同了。但我们仍然可以沿用处理无权图时记录的信息,\(d_{v}, p_{v}\) 和 Known。
解决单源最短路径问题的一般方法为 Dijkstra 算法,其是一个贪心算法 (greedy algorithm)。其核心思想为:对于每轮迭代,在所有未知顶点中选择具有最小 \(d_{v}\) 的顶点 \(v\),声明 \(s\) 到 \(v\) 的路径已经为最短路,并更新所有从 \(v\) 出发的边的终点节点的路径最小值。
既然我们要动态地更新并调用每个时刻下具有最小 \(d_{v}\) 的顶点 \(v\),那么容易想到采用优先队列来辅助算法实现,以避免每次 \(O(|V|)\) 地寻找这个最小距离顶点。
采用邻接表存储图的话,其声明、初始化和 Dijkstra 算法的伪代码如下:
typedef int Vertex;
struct TableEntry {
List Header;
int Known;
DistType Dist;
Vertex Path;
};
#define NotAVertex (-1)
typedef struct TableEntry Table[NumVertex];
void InitTable(Vertex Start, Graph G, Table T) {
ReadGraph(G, T);
for (int i = 0; i < NumVertex; i++) {
T[i].Known = False;
T[i].Dist = Infinity;
T[i].Path = NotAVertex;
}
T[Start].Dist = 0;
}
void Dijkstra(Table T) {
Vertex V, W;
while (True) {
V = smallest unknown distance vertex;
if (V == NotAVertex) {
break;
}
T[V].Known = True;
for each W adjacent to V {
if (!T[W].Known) {
if (T[V].Dist + Cvw < T[W].Dist) {
Decrease(T[W].Dist to T[V].Dist + Cvw);
T[W].Path = V;
}
}
}
}
}
如果采用优先队列维护距离最小值,那么每次查找最小值的时间复杂度即为 \(O(\log |V|)\),算法的总复杂度即为 \(O(|E| \log |V| + |V| \log |V|) = O(|E| \log |V|)\)。
具有负边值的图
如果图具有负边值,那么 Dijkstra 算法是无法解决的。因为对于一个已经入队的顶点,可能存在一个未被扩展到的顶点 \(v\),其到 \(u\) 有负的路径。这样选取从 \(s\) 到 \(v\) 再到 \(u\) 的路径就比从 \(s\) 到 \(u\) 的路径要更好。
Warning
在介绍正确的算法之前,我们先来讨论一种错误的做法。
一个朴素的想法是将每条边的边权都加上一个常数,使得每条边的边权都非负。然后使用前述算法求出最短路,再减去路径上加上的常数之和。
但这个做法的问题在于,每条路径的增加量和这条路径上的边数有关,这样做会导致边数较多的路径增加的边权和大于边数较少的路径。
接下来我们尝试提出一个算法来解决这个问题:
- 初始时,我们将 \(s\) 入队。
- 在之后的每一阶段,让一个顶点 \(v\) 出队。
- 遍历所有与 \(v\) 邻接的顶点 \(w\),找到所有满足 \(d_{w} > d_{v} + c_{v, w}\) 的顶点。
- 更新这些顶点的 \(d_{w}\) 和 \(p_{w}\),并将顶点 \(w\) 入队。
这个算法的伪代码如下:
void WeightedNegative(Table T) {
Queue Q;
Vertex V, W;
Q = CreateQueue(NumVertex); MakeEmpty(Q);
Enqueue(S, Q);
while (!IsEmpty(Q)) {
V = Dequeue(Q);
for each W adjacent to V {
if (T[V].Dist + Cvw < T[W].Dist) {
T[W].Dist = T[V].Dist + Cvw;
T[W].Path = V;
if (W is not already in Q) {
Enqueue(W, Q);
}
}
}
}
DisposeQueue(Q);
}
进一步分析这个算法,可以发现其时间复杂度是较高的。由于每个顶点最多可以出队 \(|V|\) 次,则总时间复杂度为 \(O(|E| \cdot |V|)\)。同时,一个小的改进在于,我们可以采用「状态压缩」的思想,用一个 01 串来记录每个顶点是否在队列中的情况,若一个顶点已在队列中,则对应的比特位就为 \(1\),否则为 \(0\)。这样可以有效减少队列的空间存储成本和确定元素是否在队中的所需的查询时间。
但是这个算法仍然存在一个可能的风险,即无法正确处理具有负值圈的情况。事实上,如果负值圈存在,算法会进入死循环。为了解决这个问题,我们引入一个判断。据前述分析,每个顶点最多可以出队 \(|V|\) 次,故当任意顶点出队 \(|V| + 1\) 次时跳出循环即可。这也为我们提供了一种判断图中是否有负值圈的方法。
无圈图
无圈图 (acyclic graphs) 即为没有圈的图,它具有一些良好的性质,便于我们解决一些问题。
Dijkstra 算法改进
在无圈图上使用 Dijkstra 算法求最短路时,我们不必再使用一个优先队列来维护需要扩展的节点,而是直接根据拓扑序扩展即可。
这个做法的正确性是显然的,因为无圈图上任何顶点的最短路径,只可能由在拓扑序中较其更前的顶点扩展而来。
由于不需要优先队列维护,故每次选取节点是常数时间的,此时算法的总复杂度为 \(O(|E| + |V|)\)。
关键路径分析法
无圈图另一个重要的应用是关键路径分析法 (critical path analysis),这是一种应用于动作节点图 (activity-node graph) 上的方法。
下图是一张动作节点图的示例:

可以看到,在动作节点图中,每个顶点同时记录了完成该顶点对应动作所需的时间。同时,两个顶点间的路径表示一种优先关系,边 \((v, w)\) 意味着动作 \(v\) 必须在动作 \(w\) 开始前完成。这一关系保证了动作节点图是一张无圈图。
一张动作节点图可以转化为一张事件节点图 (event-node graph),前文中动作节点图对应的事件节点图如下:

可以看到,事件节点图将动作节点图中位于顶点上的信息转换到了边上,而新图中的节点则代表整个工作可能进行到的一个「状态」。为了保证事件间的优先关系,可以发现在事件节点图的构造中引入了哑边和哑节点。
在事件节点图上,我们需要考察的是每个节点状态的最早完成时间 (the earliest completion time, EC) ,和每个节点状态能够完成而不影响总体完成时间的最晚完成时间 (the latest completion time, LC)。
根据定义,我们容易得到两个时间的递推式:
- \(EC_{1} = 0, EC_{w} = \max_{(v, w) \in E} (EC_{v} + c_{v, w})\)
- \(LC_{n} = EC_{n}, LC_{v} = \min_{(u, v) \in E} (LC_{w} - c_{v, w})\)
同样得益于无圈图的性质,我们仍然可以利用拓扑排序来完成递推求解。计算 \(EC\) 时只需按照拓扑序从前往后计算,而计算 \(LC\) 时只需倒转拓扑序从后往前计算,即可保证结果的正确性。
在求得每个节点的 EC 和 LC 后,我们就可以求得每条边对应动作的松弛时间 (slack time),即该动作可以延迟而不推迟总体完成的最大时间量。根据定义,可以得到 \(\text{Slack}_{(v, w)} = LC_{w} - EC_{v} - c_{v, w}\)。
如果一条边的松弛时间为 \(0\),则称该边为零松弛边,该边对应的动作为关键动作,即不能被延迟,必须在被扩展时马上开始以按计划结束的动作。在事件节点图中,至少存在一条完全由零松弛边组成的路径,这样的路径称作关键路径 (critical path)。
网络流问题
对于一个有向图 \(G = (V, E)\),我们给每条边赋一个边容量 \(c_{v, w}\),代表可以通过该边的最大流量。同时我们在图 \(G\) 中指定一个发点 (source) \(s\),一个收点 (sink) \(t\)。除了这两个点外,每个顶点的流入流量必须等于流出流量。最大流问题就是求从 \(s\) 到 \(t\) 可以通过的最大流量。
下图中呈现了一个有向图与其最大流的示例。

解决最大流问题的首要想法是分阶段进行。我们从图 \(G\) 开始并构造一个流图 \(G_{f}\),表示算法在任意阶段每条边已经到达的流量。开始时 \(G_{f}\) 所有的边都没有流,我们希望当算法终止时 \(G_{f}\) 包含最大流。我们再构造残余图 (residual graph) \(G_{r}\),表示算法在任意阶段每条边还能再添加多少流量。显然地,对于每一条边,我们可以从容量中减去当前流量而计算出残余的流量。\(G_{r}\) 中的边称作残余边 (residual edge)。
在每个阶段中,我们寻找图 \(G_{r}\) 中从 \(s\) 到 \(t\) 中的一条路径,这条路径称作增长通路 (augmenting path)。这条路径上的最小值边就是可以添加到流图 \(G_{f}\) 路径上每条边的流量。每一次选取增长通路并对每条边进行增加操作称作「增广」,于是最终得到的网络流可以被视为若干次增广分别得到的流的叠加。
但是我们的问题在于,这条增长路径的选取是不确定的,而我们难以用贪心等自然的方式来确定我们选取增长路径的的顺序,因为这样得到的最后的流不一定是最大流,对应的反例是好构造的。为了解决这个问题,我们要引入反向边。
对于每条边 \((u, v)\),我们都新建一条反向边 \((v, u)\)。我们约定 \(f(u, v) = -f(v, u)\),这一性质可以通过在每次增广时引入退流操作来保证,即 \(f(u, v)\) 增加时 \(f(v, u)\) 应当减少同等的量。
于是我们可以注意到,在增广的过程中,真正有意义的是 \(G_{r}\) 中的剩余容量。因为反向边流量的减少等价于反向边剩余容量的增加,这意味着我们在下一次增广中可以通过走反向边来和原先正向的增广抵消,这代表一种「反悔」的操作。而这种操作带来的「抵消」效果使得我们无需担心我们按照「错误」的顺序选择了增广路。
容易发现,只要在存在反向边的 \(G_f\) 上存在增广路,那么对其增广就可以令总流量增加;否则说明总流量已经达到最大可能值,即求得最大流。
虽然对这一算法的具体代码实现不会在本课程中展开,但我们仍然可以给出一个算法的时间复杂度上界,即 \(O(f|E|)\),其中 \(f\) 是 \(G\) 上的最大流。这是因为单次增广的时间复杂度是 \(O(|E|)\),而增广会导致总流量增加,故增广轮数不会超过 \(f\)。
最小生成树
对最小生成树的讨论一般在正边权无向图中进行。一个无向图 \(G\) 的最小生成树 (minimum spanning tree, MST) 是指一个在所有 \(G\) 的连通子图中,边权和最小的子图。
一个显然的结论是,最小生成树应当包含 \(|V| - 1\) 条边,因为这是保证图联通的最少边数,再添加任何边都会导致边权和增大。这也是这张子图是一个「树」的原因。
解决最小生成树有两个常用算法。在下文的讨论中,我们都以下图中的图 \(G\) 为例:

Prim 算法
求解最小生成树的一种方法是使其一步步地「长成」,即在每一步将一个节点当作根并往上加边。
在算法的任意时刻,一个已经在生成树中的点集 \(P\) 和未在生成树中的点集 \(Q\) 都是确定的。于是我们只需找到所有满足 \(u \in P, v \in Q\) 的边 \((u, v)\) 中边权最小的一条,并将这条边和其对应的未在生成树中的点添加到最小生成树中即可。
对于每一个顶点 \(v\),我们记录 \(d_{v}, p_{v}\) 两个值,分别是顶点 \(v\) 到生成树中所有顶点的最短边权,和导致 \(d_{v}\) 发生改变的最后顶点。而 \(d_{v}\) 的更新是简单的,只需在向生成树添加顶点 \(v\) 后,将所有与 \(v\) 邻接的,且还未在生成树中的顶点 \(w\),作更新 \(d_{w} = \min(d_{w}, c_{v, w})\)。
下图给出了在图 \(G\) 上使用 Prim 算法求最小生成树的过程:

不难发现,Prim 算法时间复杂度的主要瓶颈在于每次找到最小的树内树外边。不用堆时,算法的时间复杂度为 \(O(|V|^{2})\);用二叉堆维护树内树外边时时间复杂度为 \(O(|E| \log |V|)\)。因此,不用堆维护的 Prim 算法适用于稠密图。而使用堆维护的 Prim 算法在稀疏图上可以得到一个好的界。
Kruskal 算法
如果说 Prim 算法的出发点是顶点,即每次选取加入生成树代价最小的顶点,那么 Kruskal 算法的出发点就是边,即每次选取加入生成树代价最小的边。
具体来说,我们按照边权对图中所有的边排序,并按照从小到大的顺序遍历。如果一条边选取后在图上不会产生圈,那么就把这条边加入到最小生成树中。容易知道,按照这样的方式选取 \(|V| - 1\) 条边后,形成的子图即为最小生成树。
于是算法的关键点就在于,如何判断一条边选取后在图上是否会产生圈。这一点可以应用第五章中的不相交集这一数据结构解决。即如果一条边的两个端点在不相交集中不位于同一集合内,就表明这两个点尚未连通,这条边就是可以选取的。在选取这条边后,将其两个端点在不相交集中合并至同一集合内即可。
下图给出了在图 \(G\) 上使用 Kruskal 算法求最小生成树的过程:

我们也给出 Kruskal 算法的伪代码:
void Kruskal(Graph G) {
int EdgesAccepted;
DisjSet S;
PriorityQueue H;
Vertex U, V;
SetType Uset, Vset;
Edge E;
Initialise(S);
ReadGrapghIntoHeapArray(G, H);
BuildHeap(H);
EdgesAccepted = 0;
while (EdgesAccepted < NumVertex - 1) {
E = DeleteMin(H);
Uset = Find(U, S);
Vset = Find(V, S);
if (Uset != Vset) {
EdgesAccepted++;
SetUnion(S, Uset, Vset);
}
}
}
Note
请注意,像伪代码中一样,使用堆来维护边是可选的。在更多时候我们只需要对所有边进行一次排序即可。
无论是使用堆维护还是排序,Kruskal 算法的时间复杂度都为 \(O(|E| \log |E|)\),又因为 \(|E| = O(|V|^{2})\),故实际的时间复杂度为 \(O(|E| \log |V|)\)。
深度优先搜索
深度优先搜索 (depth-first search, DFS) 是对先序遍历的一般化。对于某个顶点 \(v\),我们先访问 \(v\),再递归地遍历所有与 \(v\) 邻接的顶点。为了避免重复搜索,我们需要记录一个顶点是否被访问过。DFS 的一般模板如下:
void DFS (Vertex V) {
Visited[V] = True;
for each W adjacent to V {
if (!Visited[V]) {
DFS(W);
}
}
}
因为这种方法保证每一个顶点和每一条边都只访问一次,所以总时间复杂度即为 \(O(|E| + |V|)\)。
DFS 可以用于解决很多问题。
无向图
当且仅当无向图是连通的,从图上任意节点出发的 DFS 能访问到每一个节点。
对于一次 DFS 的过程,我们可以对应构造出一棵深度优先生成树 (depth-first spanning tree)。具体来说,我们将这棵树的根设定为 DFS 的起点。之后,在遍历顶点 \(v\) 的每一条边 \((v, w)\) 时,如果 \(w\) 未被标记,我们就在生成树上为顶点 \(v\) 创建一个子节点 \(w\),并连接 \(v\) 和 \(w\);如果 \(w\) 已被标记,那我们就在树上从 \(v\) 出发创建一条背向边 (back edge) 连向 \(w\)。
举一个例子,对于下图中的图:

如果我们从顶点 \(A\) 开始进行 DFS,并按照逆时针顺序遍历每个顶点的边,则可以得到如下的深度优先生成树:

如果图不是连通的,那么对每个连通子图的 DFS 都将得到一棵生成树,全部生成树的集合即为深度优先生成森林 (depth-first spanning forest)。
双连通性
如果一个连通的无向图中,删去任意顶点后图仍然连通,则称该图是双连通 (biconnected) 的。
如果一个图不是双连通的,那么那些删除后使得图不再连通的顶点称作割点 (articulation point)。
更进一步地,一个图中的极大双连通子图,称作图的双连通分量 (biconnected component)。
利用 DFS,我们可以求出图中的所有割点。为方便理解,之后的讨论将在下图中的图上进行:

首先,从图中任意顶点开始,我们执行 DFS,并在每个顶点 \(v\) 被访问时给予其一个编号 \(\texttt{Num}(v)\),表示在 DFS 过程中该顶点被搜索的次序。然后,对于深度优先生成树上的每一个顶点 \(v\),寻找所有能从 \(v\) 出发,并经过若干条边和不多于 \(1\) 条背向边能访问到的节点中,\(\texttt{Num}\) 值最小的一个节点。我们将这个节点的编号记作 \(\texttt{Low}(v)\)。根据这两个定义,我们可以得到上图对应的深度优先生成树以及每个节点的 \(\texttt{Num}\) 和 \(\texttt{Low}\)(按照 \(\texttt{Num}\)/\(\texttt{Low}\) 的格式给出,且数字对应顶点字母在字母表中的顺序,如 A 对应 1)。
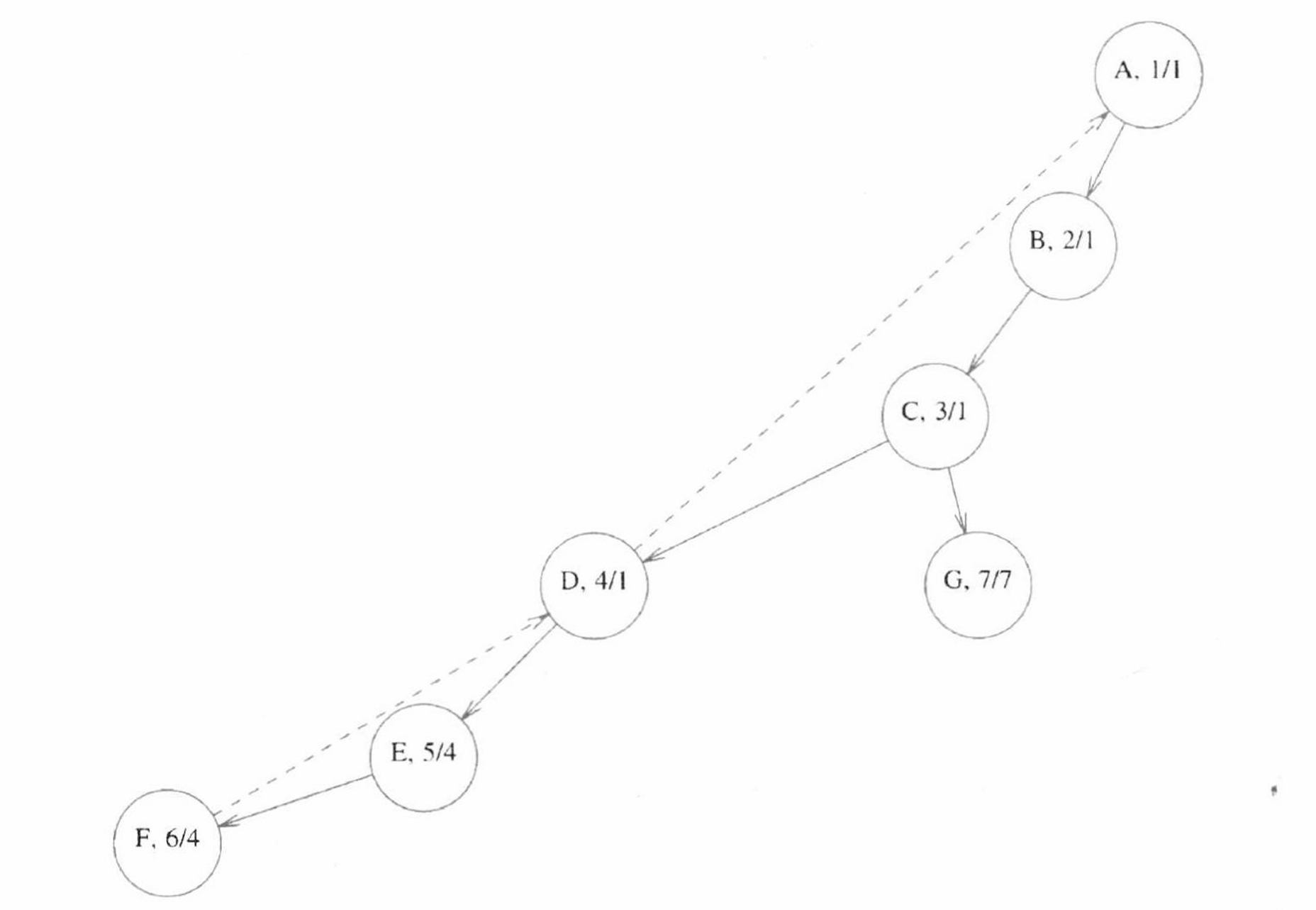
进一步分析 \(\texttt{Low}(v)\),根据 \(\texttt{Low}\) 的定义可知,\(\texttt{Low}(v)\) 的值即为以下三种量中的最小值:
- \(\texttt{Num}(v)\)
- 所有背向边 \((v, w)\) 中最小的 \(\texttt{Num}(w)\)
- 所有边 \((v, w)\) 中最小的 \(\texttt{Low}(w)\)
据此不难发现,需要先得到每个顶点的子节点的 \(\texttt{Low}\),才能得到该顶点的 \(\texttt{Low}\),因此需要利用后序遍历。另外,在算法的具体实现中,我们可以通过 \(\texttt{Num}(v)\) 和 \(\texttt{Num}(w)\) 判断边 \((v, w)\) 是一条边还是背向边。计算所有顶点的 \(\texttt{Low}\) 的时间复杂度为 \(O(|E| + |V|)\)。
在得到了深度优先生成树上每个节点的 \(\texttt{Num}\) 和 \(\texttt{Low}\) 后,我们就可以利用这些信息寻找割点。我们直接给出结论:根节点 \(r\) 是割点,当且仅当其只有一个子节点;非根节点 \(v\) 是割点,当且仅当其存在某个子节点 \(w\) 使得 \(\texttt{Low}(w) \geq \texttt{Num}(v)\)。
最后,我们给出在一次 DFS 中,完整求 \(\texttt{Num}, \texttt{Low}\) 并寻找割点的伪代码。
void FindArt(Vertex V) {
Vertex W;
Visited[V] = True;
Low[V] = Num[V] = Counter++;
for each W adjacent to V {
if (!Visited[W]) {
Parent[W] = V;
FindArt(W);
if (Low[W] >= Num[V]) {
printf("%v is an articulation point\n", v);
}
Low[V] = Min(Low[V], Low[W]);
}
else if (Parent[V] != W) { // Back edge
Low[V] = Min(Low[V], Num[W]);
}
}
}
欧拉回路
对于一个图,如果存在一条路径,使得该路径恰好经过图的每条边一次,则称该路径为欧拉路径 (Euler path);如果存在一条路径,使得该路径恰好经过图的每条边一次且起点与终点相同,则称该路径为欧拉回路 (Euler circuit)。存在欧拉回路的图称作欧拉图 (Euler Graph)。
两个重要的性质是:
- 一个图中存在欧拉回路,当且仅当该图中所有顶点的度数均为偶数。
- 一个图中存在非回路的欧拉路径,当且仅当该图中仅存在两个顶点的度数为奇数,此时这两个顶点必定为欧拉路径的起点和终点。
后一条性质可以通过将这两个度数为奇数的顶点连接在一起并通过前一条性质证明。这也启发我们,求解欧拉路径可以通过连接奇度数顶点边并求解欧拉回路得到。
接下来我们来讨论求解欧拉回路的算法。这需要利用欧拉图的另一个重要性质,即欧拉图可以被拆解为若干条不共边回路的并。
具体来说,我们先从图中用 DFS 找到一条回路作为当前回路。并从当前回路中所有剩余度数不为零的顶点出发找到一条新的回路,并将该回路与当前回路合并。重复该过程指导当前回路中所有点均无剩余度数,此时的当前回路即为欧拉回路。在具体实现中,我们应当采用合适的数据结构存储回路(如使用类链表的结构储存环),这样算法的总时间复杂度为 \(O(|E| + |V|)\)。