第七章 - 关系
约 1281 个字 预计阅读时间 4 分钟
关系及其性质
设 \(A\) 和 \(B\) 是集合,一个从 \(A\) 到 \(B\) 的二元关系 (binary relation) 是 \(A \times B\) 的子集。进一步地,一个从 \(A\) 到 \(B\) 的二元关系是集合 \(R\),当 \(a \in A, b \in B, (a, b) \in R\) 时,称 \(a\) 与 \(b\) 有关系 \(R\),记作 \(aRb\)。
函数作为关系
对于一个从集合 \(A\) 到集合 \(B\) 的函数 \(f\),一个自然的关系即为 \((a, f(a))\)。再根据函数的性质,可以知道在函数的图示中,\(A\) 的每个元素恰好是图中一个有序对的第一元素。
关系是函数的一般表示,可以用关系表示集合之间更为广泛的联系。
集合的关系
集合 \(A\) 上的关系是从 \(A\) 到 \(A\) 的关系。也即,集合 \(A\) 上的关系是 \(A \times A\) 的子集。
若 \(|A| = n\),则在 \(A\) 上存在 \(2^{n^{2}}\) 种不同的关系。
Proof
在 \(A \times A\) 中共有 \(n^{2}\) 个有序对,每个有序对可能属于或不属于关系集合中。故总的关系数量为 \(2^{n^{2}}\) 个。
关系的性质
若对每个元素 \(a \in A\) 有 \((a, a) \in R\),那么定义在集合 \(A\) 上的关系 \(R\) 称作自反的 (reflexive)。
若 \(|A| = n\),则在 \(A\) 上存在 \(2^{n(n - 1)}\) 种不同的自反关系。
Proof
如果一个定义在集合 \(A\) 上的关系是自反的,那么在 \(A \times A\) 的所有有序对中,其中所有形如 \((a, a)\) 的有序对都必须在 \(R\) 中。其余 \(n(n - 1)\) 个有序对可能属于或不属于关系集合中。故总的关系数量为 \(2^{n(n - 1)}\) 个。
若 \(\forall a, b \in A, (a, b) \in R \rightarrow (b, a) \in R\),则称定义在 \(A\) 上的关系 \(R\) 是对称的 (symmetric)。
若 \(\forall a, b \in A, ((a, b) \in R \wedge (b, a) \in R) \rightarrow (a = b)\),则称定义在 \(A\) 上的关系 \(R\) 是反对称的 (antisymmetric)。
举例来说,相等关系是对称的;小于等于关系是反对称的。
若 \(\forall a, b, c \in A, ((a, b) \in R \wedge (b, a) \in R) \rightarrow (a, c) \in R\),则定义在 \(A\) 上的关系 \(R\) 是传递的 (transitive)。
设 \(R\) 是从集合 \(A\) 到集合 \(B\) 的关系,\(S\) 是从集合 \(B\) 到集合 \(C\) 的关系。\(R\) 与 \(S\) 的合成是由有序对 \((a, c)\) 的集合构成的关系,其中 \(a \in A, c \in C\),并且存在 \(b \in B\) 使得 (a, b) \in R$ 且 \((b, c) \in S\)。我们将 \(R\) 与 \(S\) 的合成记作 \(S \circ R\)。
设 \(R\) 是集合 \(A\) 上的关系,\(R\) 的 \(n\) 次幂 \(R^{n}\) 递归地定义为 \(R^{1} = R, R^{n + 1} = R^{n} \circ R\)。
集合 \(A\) 上的关系 \(R\) 是传递的,当且仅当对 \(n = 1, 2, \cdots\),有 \(R^{n} \subseteq R\)。
Proof
充分性:\(R^{2} \subseteq R\),故 \(\forall (a, b), (b, c) \in R\),\((a, c) \in R^{2} \subseteq R\)。即得 \(R\) 是传递的。
必要性:有传递性已知 \(R^{2} \subseteq R\),后递归即证。
\(n\) 元关系及其应用
对于两个以上集合的元素之间的关系,这类关系称作 \(n\) 元关系 (\(n\)-ary relation)。
设 \(A_{1}, A_{2}, \cdots, A_{n}\) 是集合,定义在这些集合上的 \(n\) 元关系是 \(A_{1} \times A_{2} \times \cdots \times A_{n}\) 的子集。集合 \(A_{1}, A_{2}, \cdots, A_{n}\) 称作关系的域,\(n\) 称作关系的阶。
\(n\) 元关系的运算
设 \(R\) 是一个 \(n\) 元关系,\(C\) 是 \(R\) 中元素可能满足的一个条件。那么选择运算符 (selection operator) \(s_{C}\) 将 \(n\) 元关系 \(R\) 映射到 \(R\) 中满足条件 \(C\) 的所有 \(n\) 元组构成的 \(n\) 元关系。
进一步地,我们定义投影 (projection) 运算,通过删去 \(n\) 元关系中的一些域来产生一个阶较小的关系。具体来说,投影 \(P_{i_{1}, i_{2}, \cdots, i_{m}}\),其中 \(i_{1} < i_{2} < \cdots < i_{m}\),将 \(n\) 元组 \((a_{1}, a_{2}, \cdots, a_{n})\) 映射到 \(m\) 元组 \((a_{i_{1}}, a_{i_{2}}, \cdots, a_{i_{m}})\),其中 \(m \leq n\)。也就是说,投影 \(P_{i_{1}, i_{2}, \cdots, i_{m}}\) 删去了 \(n\) 元组的 \(n - m\) 个分量,保留了 \(i_{1}, i_{2}, \cdots, i_{m}\) 这 \(m\) 个分量。
另一个运算为连接 (join),它将具有某些相同域的 \(n\) 元关系组合起来。具体地说,设 \(R\) 是 \(m\) 元关系,\(S\) 是 \(n\) 元关系。连接运算 \(J_{p} (R, S)\) 是 \(m + n - p\) 元关系,其中 \(p \leq m, p \leq n\)。它包含了所有 \(m + n - p\) 元组 \((a_{1}, a_{2}, \cdots, a_{m - p}, c_{1}, c_{2}, \cdots, c_{p}, b_{1}, b_{2}, \cdots, b_{n - p})\),其中 \(m\) 元组 \((a_{1}, a_{2}, \cdots, a_{m - p}, c_{1}, c_{2}, \cdots, c_{p})\) 属于 \(R\) 且 \(n\) 元组 \((c_{1}, c_{2}, \cdots, c_{p}, b_{1}, b_{2}, \cdots, b_{n - p})\) 属于 \(W\)。也就是说,连接运算符 \(J_{p}\) 将 \(m\) 元组的后 \(p\) 个分量与 \(n\) 元组的前 \(p\) 个分量相同的第一个关系中的所有 \(m\) 元组和第二个关系的所有 \(n\) 元组组合起来产生了一个新的关系。
关系的表示
用矩阵表示关系
用矩阵表示关系的方法是自然的。假设 \(R\) 是从 \(A = \{ a_{1}, a_{2}, \cdots, a_{m} \}\) 到 \(B = \{ b_{1}, b_{2}, \cdots, b_{n} \}\) 的关系,则关系 \(R\) 可以用矩阵 \(M_{R} = [m_{ij}]\) 来表示,其中
关系的各种性质在矩阵的表示中也有体现:
- 自反性:\(M_{R}\) 主对角线上的所有元素均等于 \(1\)
- 对称性:\(M_{R} = (M_{R})^{T}\)
- 反对称性:当 \(i \neq j\) 时,\(m_{ij} = 0\) 或 \(m_{ji} = 0\)
关系的运算也和矩阵的运算相对应:
- \(M_{R_{1} \cup R_{2}} = M_{R_{1}} \vee M_{R_{2}}\)
- \(M_{R_{1} \cap R_{2}} = M_{R_{1}} \wedge M_{R_{2}}\)
- \(M_{S \circ R} = M_{R} \odot M_{S}\)
其中 \(\odot\) 表示布尔积。
用图表示关系
另一种自然的表示关系的方法是利用有向图 (directed graph)。
有关图的相关定义参见课程「数据结构基础」第六章中的相关内容。
于是,我们只需要将集合中的每个元素对应图上的顶点,每个有序对对应图中的一条有向边即可。
同样地,关系的各种性质在图的表示中有所体现:
- 自反性:图中每个顶点都有环
- 对称性:不同顶点之间的每一条边都存在一条方向相反的边
- 反对称性:两个不同顶点之间不存在两条方向相反的边
- 传递性:若存在边 \((x, y), (y, z)\),则存在边 \((x, z)\)
闭包
对于定义在集合 \(A\) 上的关系 \(R\) 和一个关系的性质 \(P\),称集合 \(A\) 中包含关系 \(R\) 且具有性质 \(P\) 的最小关系 \(S\) 为关系 \(R\) 的具有性质 \(P\) 的闭包 (closure)。也就是说,所有 \(A \times A\) 上满足条件的子集,均包含 \(S\)。
这个定义是相对抽象的,我们将通过几个实例来进一步诠释并介绍闭包的不同类型。其中最重要的三种闭包,即自反闭包、对称闭包和传递闭包。
自反闭包
集合 \(A = \{1, 2, 3\}\) 上的关系 \(R = \{(1, 1), (1, 2), (2, 1), (3, 2)\}\) 不是自反的。为了得到一个包含关系 \(R\) 的尽可能小的自反关系,只需要加入 \((2, 2) 和 (3, 3)\) 即可。因此得到的新关系 \(\{(1, 1), (1, 2), (2, 1), (2, 2), (3, 2), (3, 3)\}\) 即为 \(R\) 的自反闭包。
记 \(\Delta = \{(a, a) | a \in A\}\) 为 \(A\) 上的对角关系,则容易得到 \(A\) 上的关系 \(R\) 的自反闭包即为 \(R \cup \Delta\)。
对称闭包
有了前例,对称闭包的概念和构造是相对显然的。关系 \(R\) 的对称闭包即为 \(R \cup R^{-1}\)。
传递闭包
传递闭包的构造就不似前两者那么简便。再开始下文的讨论前,我们需要读者掌握必要的图论知识。
前文中我们指出,一个关系可以用一个有向图表示。我们先考察有向图的一个性质,即连通性,后文我们会指出连通性关系与传递闭包的联系。
设 \(R\) 是集合 \(A\) 上的关系,如果对于 \(R\) 中的任意有序对 \((a, b)\),在 \(R^{*}\) 中都存在一条长度至少为 \(1\) 的路径,那么就称 \(R^{*}\) 是 \(R\) 的连通性关系。
进一步地,对于任意的 \((a, b) \in R^{n}\),\(R^{n}\) 中都存在一条从 \(a\) 到 \(b\) 的长为 \(n\) 的路径,所以 \(R^{*}\) 是所有 \(R^{n}\) 的并集,即
在定义了连通性关系后,我们给出定理:关系 \(R\) 的传递闭包等于连通性关系 \(R^{*}\)。这一点是容易从 \(R{*}\) 的定义得到的。
从图论知识我们知道,有向图中任意两点的最短路径只会经过至多 \(n\) 条边,因此有
于是这就给出了一种可行的计算传递闭包的方法。用矩阵表示如下:
容易得到,通过这种方法计算传递闭包的时间复杂度为 \(O(n^{4})\)。
等价关系
如果在集合 \(A\) 上的关系是自反的、对称的和传递的,那么该关系是一个等价关系 (equivalence relation)。
如果两个元素 \(a\) 和 \(b\) 在等价关系 \(R\) 中满足 \(aRb\),则称这两个元素是等价的 (equivalent)。
设 \(R\) 是定义在集合 \(A\) 上的等价关系,与 \(A\) 中的一个元素 \(a\) 有关系的所有元素的几个叫做 \(a\) 的等价类 (equivalence class),记作 \([a]_{R} = \{ s | (a, s) \in R \}\)。如果 \(b \in [a]_{R}\),那么 \(b\) 称作这个等价类的代表元。
集合 \(S\) 的划分 (partition) 是 \(S\) 的不相交的非空子集构成的集合,且它们的并集就是 \(S\)。设 \(R\) 是定义在集合 \(S\) 上的等价关系,那么 \(R\) 的等价类构成 \(S\) 的划分。反之,给定 \(S\) 的划分 \(\{ A_{i} | i \in I \}\),则存在一个等价关系 \(R\) 以集合 \(A_{i} (i \in I)\) 作为其等价类。
偏序
如果定义在集合 \(S\) 上的关系 \(R\) 是自反的、反对称的和传递的,那么该关系是偏序 (partial ordering)。集合 \(S\) 与定义在其上的偏序 \(R\) 一起称作偏序集 (poset),记作 \((S, R)\)。
如果偏序集 \((S, \preceq)\) 中的元素 \(a\) 和 \(b\) 有 \(a \preceq b\) 或 \(b \preceq\),则称 \(a\) 和 \(b\) 是可比的 (comparable)。反之 \(a\) 和 \(b\) 是不可比的 (incomparable)。
如果偏序集 \((S, \preceq)\) 中的每对元素都是可比的,则 \(S\) 称作全序集 (total ordering) 或线序集 (linear ordering),\(\preceq\) 称作全序或线序。全序集也称作链。
对于偏序集 \((S, \preceq)\),如果 \(\preceq\) 是全序且 \(S\) 的每个非空子集都有一个最小元素,就称该偏序集为良序集 (well-ordered set)。
一个常用的用于描述偏序关系的工具是哈塞图 (Hasse diagram)。下图是描述偏序集 \((\{1, 2, 3, 4, 6, 8, 12\}, |)\) 的哈塞图:
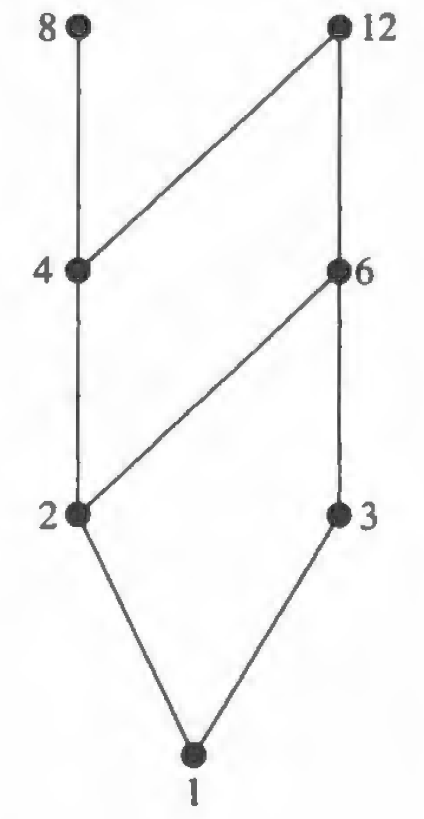
若不存在 \(b \in S\) 使得 \(a \prec b\),则称 \(a\) 是偏序集 \((S, \preceq)\) 的极大元 (maximal element)。若不存在 \(b \in S\) 使得 \(b \prec a\),则称 \(a\) 是偏序集 \((S, \preceq)\) 的极小元 (minimal element)。
若对于所有的 \(b \in S\) 有 \(b \preceq a\),则称 \(a\) 是偏序集 \((S, \preceq)\) 中的最大元 (greatest element)。若对于所有的 \(b \in S\) 有 \(a \preceq b\),则称 \(a\) 是偏序集 \((S, \preceq)\) 中的最小元 (least element)。若最大元或最小元存在,则其是唯一的。
记 \(A\) 是偏序集 \((S, \preceq)\) 的一个子集。若 \(u \in S\),且 \(\forall a \in A, a \preceq u\),则称 \(u\) 是 \(A\) 的一个上界 (upper bound)。若 \(u \in S\),且 \(\forall a \in A, u \preceq a\),则称 \(u\) 是 \(A\) 的一个下界 (lower bound)。
若 \(x\) 是子集 \(A\) 的上界,且小于 \(A\) 的任何其它上界,则称 \(x\) 是 \(A\) 的最小上界 (least upper bound)。若 \(x\) 是子集 \(A\) 的下界,且大于 \(A\) 的任何其它下界,则称 \(x\) 是 \(A\) 的最大下界 (most lower bound)。
如果一个偏序集的每对元素都有最小上界和最大下界,则称这个偏序集为格 (lattice)。
拓扑排序
这部分请参考数据结构基础 - 第六章 - 图论算法。