第八章 - 图
约 2079 个字 预计阅读时间 7 分钟
图和图模型
这部分请参考数据结构基础 - 第六章 - 图论算法。
我们给出一个表格供参考:
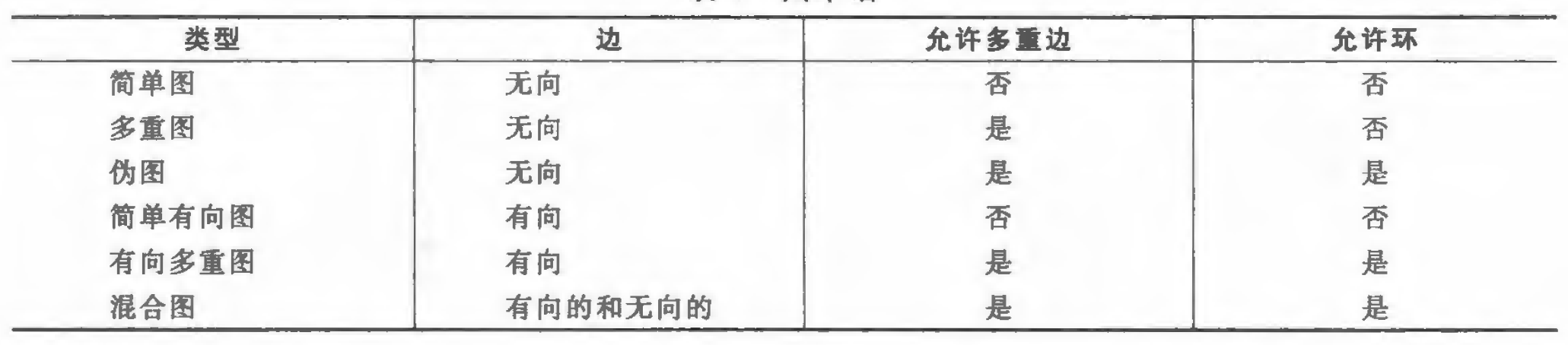
图的术语
我们先约定如下记号。
图 \(G = (V, E)\) 中,顶点 \(v\) 的所有相邻顶点的集合记作 \(N(v)\)。若 \(A\) 是 \(V\) 的子集,我们用 \(N(A)\) 表示图 \(G\) 中至少和 \(A\) 中一个顶点相邻的所有顶点的集合,即 \(N(A) = \cup_{v \in A} N(v)\)。
顶点 \(v\) 的度 (degree) 是与该顶点相关联的边的数目,记作 \(\deg (v)\)。在带有有向边的图里,以 \(v\) 作为终点的边数称作顶点 \(v\) 的入度,记作 \(\deg^{-} (v)\);以 \(v\) 作为起点的边数称作顶点 \(v\) 的出度,记作 \(\deg^{+} (v)\)。
根据这些定义,我们可以得到许多有关图的性质。
设 \(G = (V, E)\) 是有 \(m\) 条边的无向图,则 \(2m = \sum_{v \in V} \deg (v)\)。这个结论被称作握手定理 (The handshaking theorem)。
无向图有偶数个度为奇数的顶点。
对于有向图 \(G = (V, E)\),有 \(\sum_{v \in V} \deg^{-} (v) = \sum_{v \in V} \deg^{+} (v) = |E|\)。
这些性质都是容易从定义得到的。
几种特殊的图
完全图、圈图、轮图、立方体图
在每对不同顶点间恰有一条边的简单图称作完全图 (complete graph),有 \(n\) 个顶点的完全图记作 \(K_{n}\)。
由 \(n (n \geq 3)\) 个顶点 \(v_{1}, v_{2}, \cdots, v_{n}\) 以及边 \(\{ v_{1}, v_{2} \}, \{ v_{2}, v_{3} \}, \cdots, \{ v_{n - 1}, v_{n} \}, \{ v_{n}, v_{1} \}\) 组成的图称作圈图 (cycle graph),记作 \(C_{n}\)。
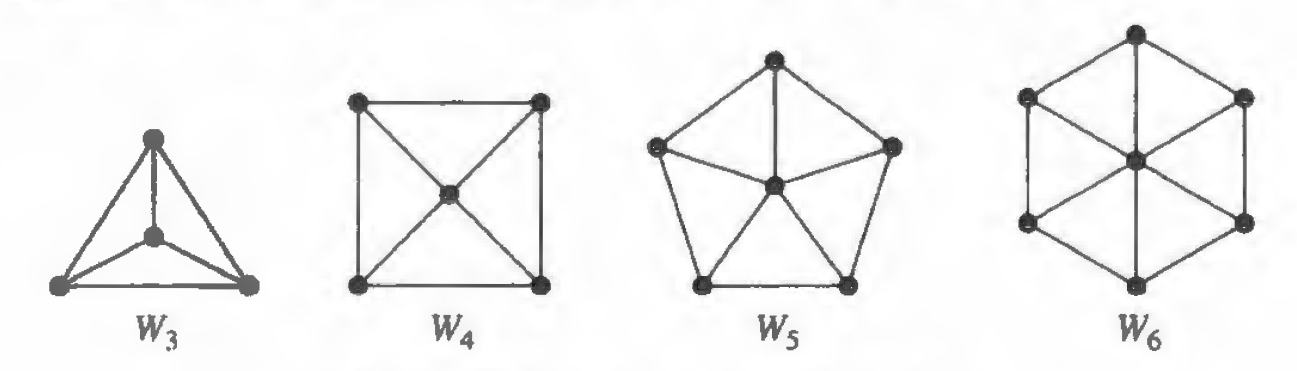
对于圈图 \(C_{n}, n \geq 3\),添加一个新顶点,并且该顶点与 \(C_{n}\) 中的 \(n\) 个顶点均相连,则得到轮图 (wheel graph),记作 \(W_{n}\)。下图展示了一些轮图:
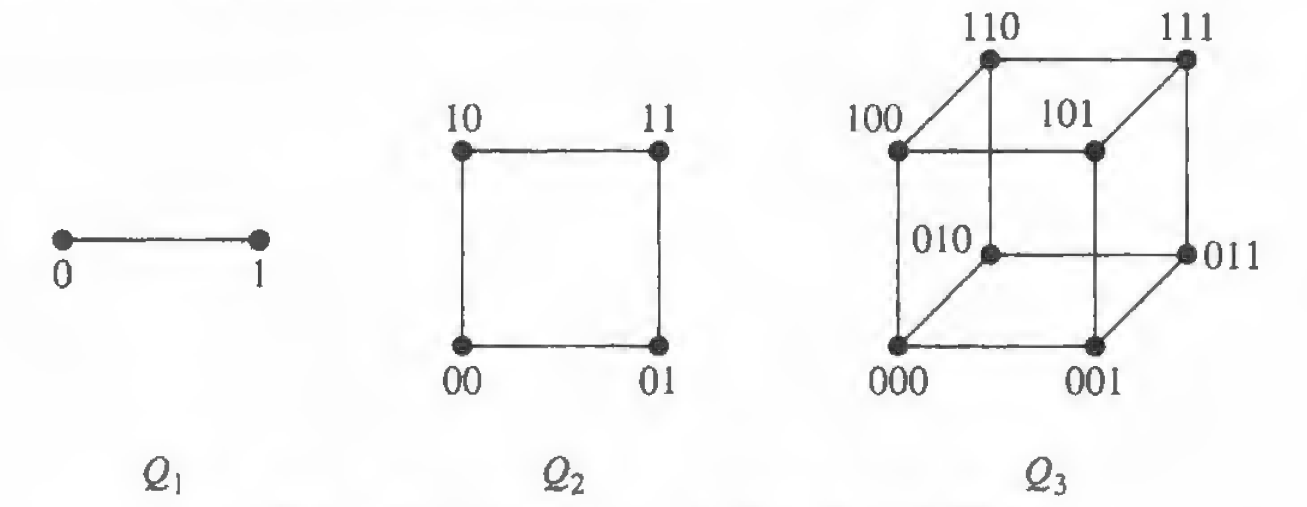
若一个图含有 \(2^{n}\) 个顶点,且两个顶点相邻当且仅当其下标数的二进制表示仅有一位不同,则这样的图称作\(n\) 立方体图 (\(n\)-cube graph)。下图展示了一些立方体图:
二分图
若简单图 \(G\) 的顶点集可以被分成两个不相交的非空集合 \(V_{1}\) 和 \(V_{2}\),使得图中的每一条边的两个端点刚好分别属于 \(V_{1}\) 和 \(V_{2}\),则称 \(G\) 为二分图 (bipartite graph)。此时称 \((V_{1}, V_{2})\) 为 \(G\) 的顶点集的一个二部划分。
一个简单图是二分图,当且仅当能够对图中的每个顶点赋予两种不同的颜色之一,并使得没有两个相邻的顶点被赋予相同的颜色。
若简单图的顶点集划分成分别含有 \(m\) 和 \(n\) 个顶点的两个子集,且两个顶点之间有边当且仅当两个顶点分别属于两个子集,则称该图为完全二分图 (complete bipartite graph),记作 \(K_{m, n}\)。
在简单图 \(G = (V, E)\) 中的一个匹配 (matching) \(M\) 是边集 \(E\) 的子集,该自己种没有两条边关联相同的顶点。包含最多边数的一个匹配称作最大匹配 (maximum matching)。若一个二分图的划分为 \((V_{1}, V_{2})\),且 \(|M| = |V_{1}|\),则称匹配 \(M\) 是从 \(V_{1}\) 到 \(V_{2}\) 的一个完全匹配 (complete matching)。
带有二部划分 \((V_{1}, V_{2})\) 的二分图 \(G = (V, E)\) 中存在从 \(V_{1}\) 到 \(V_{2}\) 的一个完全匹配,当且仅当对于 \(V_{1}\) 的所有子集 \(A\),有 \(|N(A)| \geq |A|\)。这一定理称作霍尔婚姻定理 (Hall's marriage theorem)。
从旧图构造新图
当从图中删除了边和顶点,不删除所保留便的端点时,就得到一个更小的图,这样的图称作原图的子图 (subgraph)。形式化地说,图 \(G = (V, E)\) 的子图是图 \(H = (W, F)\),其中 \(W \subset V\) 且 \(F \subset E\)。若 \(H \neq G\),则称图 \(G\) 的子图 \(H\) 是 \(G\) 的贞子图。
已知一个图的顶点集合,我们可以由图中的顶点和链接这些顶点的边得到这个图的子图。具体来说,令 \(G = (V, E)\) 是一个简单图,图 \((W, F)\) 是由顶点集 \(V\) 的子集 \(W\) 导出的子图,其中边集 \(F\) 包含 \(E\) 中的一条边当且仅当这条边的两个端点都在 \(W\) 中。
对于两个或更多的图,包含这些图的所有顶点和边的新图称作这些图的并图 (union graph)。形式化地说,两个简单图 \(G_{1} = (V_{1}, E_{1})\) 和 \(G_{2} = (V_{2}, E_{2})\) 的并图是带有顶点集 \(V_{1} \cup V_{2}\) 和边集 \(E_{1} \cup E_{2}\) 的简单图。\(G_{1}\) 和 \(G_{2}\) 的并图表示为 \(G_{1} \cup G_{2}\)。
图的表示
常用的两种表示图的方式是邻接表 (adjacency table) 和邻接矩阵 (adjacency matrix)。其中前者更适于表示稀疏图 (sparse graph),后者更适于表示稠密图 (dense graph)。
另一种表示图的常用方式是关联矩阵 (incidence matrix)。设 \(G = (V, E)\) 是无向图,\(v_{1}, v_{2}, \cdots, v_{n}\) 是图 \(G\) 的顶点,\(e_{1}, e_{2}, \cdots, e_{m}\) 是图 \(G\) 的边。则图 \(G\) 的关联矩阵是 \(n \times m\) 的矩阵 \(M = [m_{ij}]\),其中
图的同构
设 \(G_{1} = (V_{1}, E_{1})\) 和 \(G_{2} = (V_{2}, E_{2})\) 是简单图。若存在从 \(V_{1}\) 到 \(V_{2}\) 的双射 \(f\),且对 \(V_{1}\) 中所有的点对 \((a, b)\) 来说,\(a\) 和 \(b\) 在 \(G_{1}\) 中相邻当且仅当 \(f(a)\) 和 \(f(b)\) 在 \(G_{2}\) 中相邻,则称 \(G_{1}\) 和 \(G_{2}\) 是同构 (isomorphism) 的。
判定两个图同构往往是一件困难的事情,但说明两个图不同构并不困难。只需要找到一个在同构中保持不变的图属性,并表明两个图的该属性不同即可。这样的属性称作同构不变量 (invariant for graph isomorphism)。
连通性
这部分内容请参考 OI Wiki 的相关内容。
欧拉通路与哈密顿通路
这部分内容请参考 OI Wiki 中欧拉通路和哈密顿通路的相关内容。
最短通路问题
这部分请参考数据结构基础 - 第六章 - 图论算法。
平面图
若可以在平面中画出一个图而便没有任何交叉,则这个图是平面图 (planar graph)。这种画法称作这个图的平面表示。
欧拉公式
一个图的平面表示把平面分割成一些面 (region),包括一个无界的面。一个重要的结论是,设 \(G\) 是带 \(e\) 条边和 \(v\) 个顶点的联通平面简单图,\(r\) 是 \(G\) 的平面表示中的面数,则 \(r = e - v + 2\)。这个结论被称作欧拉公式 (Euler's formula)。
根据这一公式,可以得到一些平面图的推论:
- 若 \(G\) 是 \(e\) 条边和 \(v\) 个顶点的连通平面简单图,其中 \(v \geq 3\),则 \(e \leq 3v - 6\)。
- 若 \(G\) 是连通平面简单图,则 \(G\) 中有古树不超过 \(5\) 的顶点。
- 若 \(G\) 是 \(e\) 条边和 \(v\) 个顶点的连通平面简单图,其中 \(v \geq 3\) 且没有长度为 \(3\) 的回路,则 \(e \leq 2v - 4\)。
库拉图斯基定理
若一个图是平面图,则通过删除一条边 \(\{u, v\}\) 并且添加一个新顶点 \(w\) 和两条边 \(\{u, w\}\) 与 \(\{w, v\}\) 获得的任何图也是平面图。这样的操作称作初等细分 (elementary subdivision)。托可以从相同的图通过一系列初等细分得到图 \(G_{1}\) 和图 \(G_{2}\),则称它们是同胚 (homeomorphic) 的。
一个重要的定理是:一个图是非平面图当且仅当它包含一个同胚于 \(K_{3, 3}\) 或 \(K_{5}\) 的子图。这个定理称作库拉图斯基定理 (Kuratowski's theorem)。
图着色
简单图的着色 (colouring) 是对该图的每个顶点都指定一种颜色,使得没有两个相邻的顶点颜色相同。
图的着色数 (chromatic number) 是着色这个图所需要的最少颜色数。图 \(G\) 的着色数记作 \(\chi (G)\)。
一个著名的定理,即四色定理 (The four colour theorem) 指出:平面图的着色数不超过 \(4\)。