第八章 - 假设检验

约 5103 个字预计阅读时间 17 分钟

假设检验的基本思想

问题的提出

统计假设简称为假设，通常用字母 \(H\) 表示。一般我们同时提出两个完全相反的假设，习惯上把其中的一个称作原假设 (null hypothesis) 或零假设，用 \(H_{0}\) 表示；把另一个假设称作备择假设 (alternative hypothesis) 或对立假设，用 \(H_{1}\) 表示。一般地，在有关参数的假设检验中，备择假设是我们根据样本资料想得到支持的假设。

关于总体参数 \(\theta\) 的假设，有三种情况：

\(H_{0}: \theta \geq \theta_{0}, H_{1}: \theta < \theta_{0}\)
\(H_{0}: \theta \leq \theta_{0}, H_{1}: \theta > \theta_{0}\)
\(H_{0}: \theta = \theta_{0}, H_{1}: \theta \neq \theta_{0}\)

其中 \(\theta_{0}\) 是已知常数。以上三种情况中，前两种假设的检验称作单侧检验 (one-sided test)；第三种假设的检验称作双侧检验 (two-sided test)。

此外，单侧检验还有下列两种形式：

\(H_{0}: \theta = \theta_{0}, H_{1}: \theta < \theta_{0}\)
\(H_{0}: \theta = \theta_{0}, H_{1}: \theta > \theta_{0}\)

检验统计量和拒绝域

一般地，在假设检验问题中，若寻找到某个统计量，其取值大小和原假设 \(H_{0}\) 是否成立有密切联系，我们称之为该假设检验问题的检验统计量 (test statistic)，对应于拒绝原假设 \(H_{0}\) 的样本值范围称作拒绝域 (rejection region)，记作 \(W\)。拒绝域 \(W\) 的补集 \(\overline{W}\) 称作接受域 (acceptance region)。如果样本落入拒绝域 \(W\) 内，就拒绝原假设 \(H_{0}\)；如果样本未落入拒绝域 \(W\) 内，就接受原假设 \(H_{0}\)。

因此，对于一个假设检验问题，给出一个检验规则，相当于在样本空间中划分出一个子集作为检验的拒绝域；反之，给出一个拒绝域也就给出了一个检验规则。故如何选取检验的拒绝域就成为假设检验的一个关键问题。

两类错误

在给出具体的假设检验方法之前，我们需要先讨论假设检验问题中可能出现的两类错误。

根据样本推断总体，由于抽样的随机性，所做的结论不能保证绝对不犯错误，而只能以较大的概率保证其正确性。在假设检验推断中可能出现下列四种情形：

拒绝了一个错误的原假设
接受了一个真实的原假设
拒绝了一个真实的原假设
接受了一个错误的原假设

其中前两种情形是正确的。第三种情形称作第 I 类错误 (type I error)，也称作弃真错误；第四种情形称作第 II 类错误 (type II error)，也称作存伪错误。通常，用 \(\alpha\) 表示犯第 I 类错误的概率，用 \(\beta\) 表示犯第 II 类错误的概率。具体地，有

\[\begin{aligned} \alpha & = P(\text{第 I 类错误}) = P\{ \text{拒绝 } H_{0} | H_{0} \text{ 是真实的} \} \\ \beta & = P(\text{第 II 类错误}) = P\{ \text{接受 } H_{0} | H_{0} \text{ 是错误的} \} \end{aligned}\]

一般来说，当样本容量固定时，犯这两类错误的概率是相互制约的，使其中一者减小往往伴随着另一者增大。若要同时使得犯两类错误的概率都减小，就必须增大样本容量。

鉴于上述情况，奈曼和皮尔逊提出：首先控制犯第 I 类错误的概率，即选定一个常数 \(\alpha \in (0, 1)\)，要求犯第 I 类错误的概率不超过 \(\alpha\)；然后在满足这个约束条件的检验中，再寻找使得犯第 II 类错误的概率尽量小的检验。这就是假设检验理论中的奈曼-皮尔逊原则 (Neyman-Pearson lemma)，其中的常数 \(\alpha\) 称作显著性水平 (significance level)。

\(P\)-值与统计显著性

在原假设和备择假设中，我们只考虑检验统计量是否落在拒绝域内。但直观上，检验统计量与临界值的距离也会影响我们拒绝或接受原假设的把握。例如当检验统计量落在拒绝域内时，其值离临界值越远，我们拒绝原假设的理由就越充分，检验越显著。

我们采用 \(P\)-值来衡量这一现象，当原假设 \(H_{0}\) 为真时，检验统计量取比观察到的结果更为极端的数值的概率称作 \(P\)-值。在实际运用中，通过计算 \(P\)-值来衡量拒绝 \(H_{0}\) 的理由是否充分。\(P\)-值较小说明观察到的结果在一次实验中发生的可能性较小，\(P\)-值越小，拒绝 \(H_{0}\) 的理由越充分；\(P\)-值较大说明观察到的结果在一次实验中发生的可能性较大，所以没有足够的理由拒绝 \(H_{0}\)。

当假设检验的显著性水平为 \(\alpha\) 时，若 \(P\)-值小于等于 \(\alpha\)，则拒绝原假设，此时我们称检验结果在显著性水平 \(\alpha\) 下是统计显著 (statistically significant) 的。

可以说 \(P\)-值提供了比显著性水平 \(\alpha\) 更多的信息，根据 \(P\)-值，我们可以判定在任何给定的显著性水平下检验结果是否显著。

处理假设检验问题的基本步骤

一般的假设检验问题我们可按下列步骤进行：

根据实际问题提出原假设和备择假设；
提出检验统计量和拒绝域的形式；
根据奈曼-皮尔逊原则和给定的显著性水平 \(\alpha\)，求出拒绝域 \(W\) 中的临界值；
根据实际样本值作出判断。

如果从 \(P\)-值出发考察，步骤也可如下进行：

根据实际问题提出原假设和备择假设；
提出检验统计量和拒绝域的形式；
计算检验统计量的观测值和 \(P\)-值；
根据给定的显著性水平 \(\alpha\) 作出判断。

单个正态总体参数的假设检验

设正态总体 \(X \sim N(\mu, \sigma^{2})\)，\(X_{1}, X_{2}, \cdots, X_{n}\) 是来自该总体的样本，记

\[\bar{X} = \frac{1}{n} \sum_{i = 1}^{n} X_{i}, S^{2} = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}\]

有关参数 \(\mu\) 的假设检验

\(\sigma^{2}\) 已知

先考虑双侧假设问题

\[H_{0}: \mu = \mu_{0}, H_{1}: \mu \neq \mu_{0}\]

其中 \(\mu_{0}\) 是已知的常量。此时我们取检验统计量

\[Z = \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}}\]

当原假设 \(H_{0}\) 成立，即 \(\mu = \mu_{0}\) 时，\(Z \sim N(0, 1)\)，根据奈曼-皮尔逊原则，在给定的显著性水平 \(\alpha\) 下，检验的拒绝域为

\[W = \left\{ |Z| = \left| \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}} \right| \geq z_{\frac{\alpha}{2}} \right\}\]

对给定样本值 \(x_{1}, x_{2}, \cdots, x_{n}\)，检验统计量 \(Z\) 的取值 \(z_{0} = \frac{\bar{x} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}}\)。当 \(|z_{0}| \geq z_{\frac{\alpha}{2}}\) 时，就作出拒绝原假设的判断，即认为根据当前样本资料，我们有 \(1 - \alpha\) 的把握认为 \(\mu \neq \mu_{0}\)；否则不拒绝原假设。

我们也可以通过计算 \(P\)-值来做出判断，其中

\[P\text{-值} = P_{H_{0}} \{ |Z| \geq |z_{0}| \} = 2 P_{H_{0}} \{ Z \geq |z_{0}| \} = 2(1 - \Phi(|z_{0}|))\]

当 \(P\)-值小于等于给定的显著性水平时，拒绝原假设，否则不能拒绝原假设。

对于左侧假设问题

\[H_{0}: \mu \geq \mu_{0}, H_{1}: \mu < \mu_{0}\]

检验统计量仍为

\[Z = \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}}\]

当原假设 \(H_{0}\) 成立，即 \(\mu \geq \mu_{0}\) 时，\(Z\) 取值偏大，检验的拒绝域为

\[W = \left\{ Z = \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}} \leq c \right\}\]

其中临界值 \(c\) 满足奈曼-皮尔逊原则。首先我们来计算犯第 I 类错误的概率：

\[\alpha(\mu, c) = P\{ \text{拒绝 } H_{0} | H_{0} \text{ 是真实的} \} = P \left\{ \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}} \leq c | \mu \geq \mu_{0} \right\}\]

注意到此时 \(Z\) 不服从标准正态分布，而是

\[Z \sim N \left( \frac{\mu - \mu_{0}}{\frac{\sigma}{\sqrt{n}}}, 1 \right), \mu \geq \mu_{0}\]

因此

\[\alpha(\mu, c) = \Phi \left( c - \frac{\mu - \mu_{0}}{\frac{\sigma}{\sqrt{n}}} \right), \mu \geq \mu_{0}\]

如果假设为 \(H_{0}: \mu = \mu_{0}, H_{1}: \mu < \mu_{0}\)，那么犯第 I 类错误的概率为 \(\alpha(\mu_{0}, c)\)。从这一点来看，两个假设检验是有区别的。

显然，\(\alpha(\mu, c)\) 关于 \(\mu\) 是严格减函数，为使犯第 I 类错误的概率不超过给定的显著性水平 \(\alpha\)，需满足

\[\sup_{\mu \geq \mu_{0}} \alpha(\mu, c) = \alpha(\mu_{0}, c) = \Phi(c) \leq \alpha\]

又根据奈曼-皮尔逊原则，当上式中等号成立时，犯第 II 类错误的概率最小。因此，应取 \(c = z_{1 - \alpha} = -z_{\alpha}\)，故左侧假设检验问题的拒绝域为

\[W = \left\{ Z = \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}} \leq -z_{\alpha} \right\}\]

我们也可以通过计算 \(P\)-值来做出判断，其中

\[P\text{-值} = \sup_{\mu \geq \mu_{0}} P \{ Z \leq z_{0} \} = P \{ Z \leq z_{0} | \mu = \mu_{0} \} = \Phi(z_{0})\]

当 \(P\)-值小于等于给定的显著性水平 \(\alpha\) 时，拒绝原假设 \(H_{0}\)，否则不能拒绝原假设 \(H_{0}\)。

类似地，对于右侧假设问题

\[H_{0}: \mu \leq \mu_{0}, H_{1}: \mu > \mu_{0}\]

检验的拒绝域为

\[W = \left\{ Z = \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}} \geq z_{\alpha} \right\}\]

\(P\)-值为

\[P\text{-值} = \sup_{\mu \leq \mu_{0}} P \{ Z \geq z_{0} \} = P \{ Z \geq z_{0} | \mu = \mu_{0} \} = 1 - \Phi(z_{0})\]

上述检验称作 \(Z\) 检验。

\(\sigma^{2}\) 未知

当参数 \(\sigma^{2}\) 未知时，我们不能采用 \(Z\) 检验，而是需要用样本方差 \(S^{2}\) 来代替 \(\sigma^{2}\)，从而得到检验统计量

\[T = \frac{\bar{X} - \mu_{0}}{\frac{S}{\sqrt{n}}}\]

根据 \(t\) 分布的性质，我们知道

\[T = \frac{\bar{X} - \mu_{0}}{\frac{S}{\sqrt{n}}} \sim t(n - 1)\]

于是当给定样本值 \(x_{1}, x_{2}, \cdots, x_{n}\) 时，检验统计量 \(t_{0} = \frac{\bar{x} - \mu_{0}}{\frac{S}{\sqrt{n}}}\)。根据 \(t\) 分布，我们可计算出相应的拒绝域和 \(P\)-值。

双侧假设问题

\[H_{0}: \mu = \mu_{0}, H_{1}: \mu \neq \mu_{0}\]

拒绝域为

\[W = \left\{ |T| = \left| \frac{\bar{X} - \mu_{0}}{\frac{S}{\sqrt{n}}} \right| \geq t_{\frac{\alpha}{2}} (n - 1) \right\}\]

\(P\)-值为

\[P\text{-值} = 2 P \{ t(n - 1) \geq |t_{0}| \}\]

左侧假设问题

\[H_{0}: \mu \geq \mu_{0}, H_{1}: \mu < \mu_{0}\]

拒绝域为

\[W = \left\{ T = \frac{\bar{X} - \mu_{0}}{\frac{S}{\sqrt{n}}} \leq -t_{\alpha} (n - 1) \right\}\]

\(P\)-值为

\[P\text{-值} = \sup_{\mu \geq \mu_{0}} P \{ T \leq t_{0} \} = P \{ t(n - 1) \leq t_{0} \}\]

右侧假设问题

\[H_{0}: \mu \leq \mu_{0}, H_{1}: \mu > \mu_{0}\]

拒绝域为

\[W = \left\{ T = \frac{\bar{X} - \mu_{0}}{\frac{S}{\sqrt{n}}} \geq t_{\alpha} (n - 1) \right\}\]

\(P\)-值为

\[P\text{-值} = \sup_{\mu \leq \mu_{0}} P \{ T \leq t_{0} \} = P \{ t(n - 1) \geq t_{0} \}\]

上述检验称作 \(t\) 检验。

成对数据的 \(t\) 检验

对于成对数据样本 \((X_{1}, Y_{1}), (X_{2}, Y_{2}), \cdots, (X_{n}, Y_{n})\)，\(X_{i}\) 和 \(Y_{i}\) 一般不独立，且 \(X_{1}, X_{2}, \cdots, X_{n}\) 不能看作是来自同一个正态总体的样本，\(Y_{1}, Y_{2}, \cdots, Y_{n}\) 也不能看作是来自同一个正态总体的样本。

此时，我们一般考察差值 \(D_{i} = X_{i} - Y_{i}, i = 1, 2, \cdots, n\)。我们可以将 \(D_{1}, D_{2}, \cdots, D_{n}\) 看作是来自同一个正态总体 \(N(\mu_{D}, \sigma_{D}^{2})\) 的样本。所以，对成对数据差的假设检验可以转化为对单个正态总体均值 \(\mu_{D}\) 的假设检验。

有关参数 \(\sigma^{2}\) 的假设检验

我们不妨设参数 \(\mu\) 是未知的，其假设问题包括

双侧假设：\(H_{0}: \sigma^{2} = \sigma_{0}^{2}, H_{1}: \sigma^{2} \neq \sigma_{0}^{2}\)
左侧假设：\(H_{0}: \sigma^{2} \geq \sigma_{0}^{2}, H_{1}: \sigma^{2} < \sigma_{0}^{2}\)
右侧假设：\(H_{0}: \sigma^{2} \leq \sigma_{0}^{2}, H_{1}: \sigma^{2} > \sigma_{0}^{2}\)

其中 \(\sigma_{0}^{2}\) 是已知的常量。此时 \(\sigma^{2}\) 的无偏估计量

\[S^{2} = \frac{1}{n - 1} \sum_{i = 1}^{n} (X_{i} - \bar{X})^{2}\]

且 \(\frac{(n - 1) S^{2}}{\sigma^{2}} \sim \chi^{2}(n - 1)\)。因此，可取检验统计量为

\[\chi^{2} = \frac{(n - 1) S^{2}}{\sigma_{0}^{2}}\]

当 \(\sigma^{2} = \sigma_{0}^{2}\) 时，检验统计量 \(\chi^{2}\) 的分布是已知的，\(\chi^{2} \sim \chi^{2} (n - 1)\)。在给定显著性水平 \(\alpha\) 时，有检验拒绝域：

双侧检验：\(W = \{ \chi^{2} \geq \chi_{\frac{\alpha}{2}}^{2} (n - 1) \}\) 或 \(W = \{ \chi^{2} \leq \chi_{1 - \frac{\alpha}{2}}^{2} (n - 1) \}\)
左侧检验：\(W = \{ \chi^{2} \leq \chi_{1 - \alpha}^{2} (n - 1) \}\)
右侧检验：\(W = \{ \chi^{2} \geq \chi_{\alpha}^{2} (n - 1) \}\)

为了计算 \(P\)-值，将样本值代入后得到检验统计量的值记作 \(\chi_{0}^{2}\)，即 \(\chi_{0}^{2} = \frac{(n - 1) s^{2}}{\sigma_{0}^{2}}\)，记

\[p_{0} = P_{\sigma^{2} = \sigma_{0}^{2}} \left\{ \frac{(n - 1) S^{2}}{\sigma_{0}^{2}} \leq \frac{(n - 1) s^{2}}{\sigma_{0}^{2}} \right\} = P \{ \chi^{2} (n - 1) \leq \chi_{0}^{2} \}\]

双侧检验：\(P\text{-值} = 2 \min \{ p_{0}, 1 - p_{0} \}\)
左侧检验：\(P\text{-值} = p_{0}\)
右侧检验：\(P\text{-值} = 1 - p_{0}\)

我们称上述检验为 \(\chi^{2}\) 检验。

两个正态总体参数的假设检验

比较两个正态总体均值的假设检验

设正态总体 \(X \sim N(\mu_{1}, \sigma_{1}^{2}), Y \sim N(\mu_{2}, \sigma_{2}^{2})\)，\(X_{1}, X_{2}, \cdots, X_{n}\) 和 \(Y_{1}, Y_{2}, \cdots, Y_{n}\) 分别是来自这两个总体的独立样本。记

\[\begin{aligned} & \bar{X} = \frac{1}{n_{1}} \sum_{i = 1}^{n_{1}} X_{i}, & S_{1}^{2} = \frac{1}{n_{1} - 1} \sum_{i = 1}^{n_{1}} (X_{i} - \bar{X})^{2} \\ & \bar{Y} = \frac{1}{n_{2}} \sum_{i = 1}^{n_{2}} Y_{i}, & S_{2}^{2} = \frac{1}{n_{2} - 1} \sum_{i = 1}^{n_{2}} (Y_{i} - \bar{Y})^{2} \end{aligned}\]

考虑双侧假设问题：

\[H_{0}: \mu_{1} = \mu_{2}, H_{1}: \mu_{1} \neq \mu_{2}\]

显然，当原假设 \(H_{0}\) 成立时，两样本均值取值应比较接近，即 \(|\bar{X} - \bar{Y}|\) 取值较小，因此我们可取检验统计量为 \(\bar{X} - \bar{Y}\)。接下来，我们分几种情况讨论。

\(\sigma_{1}\) 和 \(\sigma_{2}\) 已知

由先前的定理可知，此时 \(\bar{X} - \bar{Y} \sim N(\mu_{1} - \mu_{2}, \frac{\sigma_{1}^{2}}{n_{1}} + \frac{\sigma_{2}^{2}}{n_{2}})\)。那么当 \(H_{0}\) 成立时，\(\frac{\bar{X} - \bar{Y}}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}} + \frac{\sigma_{2}^{2}}{n_{2}}}} \sim N(0, 1)\)。此时采用 \(Z\) 检验，可得拒绝域为

\[W = \left\{ \frac{\bar{X} - \bar{Y}}{\sqrt{\frac{\sigma_{1}^{2}}{n_{1}} + \frac{\sigma_{2}^{2}}{n_{2}}}} \geq z_{\frac{\alpha}{2}} \right\}\]

\(P\)-值为

\[P\text{-值} = P_{H_{0}} \{ |Z| \geq |z_{0}| \} = 2(1 - \Phi(|z_{0}|))\]

其中 \(Z \sim N(0, 1)\)，\(z_{0}\) 为给定样本值时检验统计量的取值。

\(\sigma_{1}\) 和 \(\sigma_{2}\) 相等且未知

当两总体的方差相同，即 \(\sigma_{1}^{2} = \sigma_{2}^{2} = \sigma^{2}\)，但未知时，我们可以取 \(\sigma^{2}\) 的无偏估计量

\[S_{w}^{2} = \frac{(n_{1} - 1) S_{1}^{2} + (n_{2} - 1) S_{2}^{2}}{n_{1} + n_{2} - 2}\]

可取检验统计量为

\[T = \frac{\bar{X} - \bar{Y}}{S_{w} \sqrt{\frac{1}{n_{1}} + \frac{1}{n_{2}}}}\]

当 \(H_{0}\) 成立时，\(T \sim t(n_{1} + n_{2} - 2)\)，则检验的拒绝域为

\[W = \{ |T| \geq t_{\frac{\alpha}{2}}(n_{1} + n_{2} - 2) \}\]

\(P\)-值为

\[P\text{-值} = P_{H_{0}} \{ |T| \geq |t_{0}| \} = 2 P \{ t(n_{1} + n_{2} - 2) \geq |t_{0}| \}\]

其中 \(t_{0}\) 为给定样本值时检验统计量 \(T\) 的取值。

我们称上述检验为两样本精确 \(t\) 检验。

\(\sigma_{1}\) 和 \(\sigma_{2}\) 未知

我们分别以两样本方差 \(S_{1}^{2}, S_{2}^{2}\) 作为 \(\sigma_{1}^{2}, \sigma_{2}^{2}\) 的无偏估计。

当样本容量 \(n_{1}\) 和 \(n_{2}\) 充分大时，可取检验统计量为

\[T = \frac{\bar{X} - \bar{Y}}{\sqrt{\frac{S_{1}^{2}}{n_{1}} + \frac{S_{2}^{2}}{n_{2}}}}\]

可以证明当原假设 \(H_{0}\) 成立时，\(T\) 渐进服从标准正态分布 \(N(0, 1)\)，则检验拒绝域为

\[W = \{ |T| \geq z_{\frac{\alpha}{2}} \}\]

\(P\)-值为

\[P\text{-值} = P_{H_{0}} \{ |T| \geq |t_{0}| \} = 2 P \{ Z \geq |t_{0}| \}\]

其中 \(Z \sim N(0, 1)\)，\(t_{0}\) 为给定样本值时检验统计量的取值。

对于有限小样本，仍然取检验统计量为

\[T = \frac{\bar{X} - \bar{Y}}{\sqrt{\frac{S_{1}^{2}}{n_{1}} + \frac{S_{2}^{2}}{n_{2}}}}\]

可以证明当原假设 \(H_{0}\) 成立时，\(T\) 近似服从自由度为 \(k\) 的 \(t\) 分布，其中

\[k = \left\lfloor \frac{\left( \frac{S_{1}^{2}}{n_{1}} + \frac{S_{2}^{2}}{n_{2}} \right)^{2}}{\frac{(S_{1}^{2})^{2}}{n_{1}^{2} (n_{1} - 1)} + \frac{(S_{2})^{2}}{n_{2}^{2} (n_{2} - 1)}} \right\rfloor\]

在实际应用中，也常用 \(\min \{ n_{1} - 1, n_{2} - 1 \}\) 近似代替上述自由度 \(k\)。此时检验的拒绝域为

\[W = \{ |T| \geq t_{\frac{\alpha}{2}} (k) \}\]

\(P\)-值为

\[P\text{-值} = P_{H_{0}} \{ |T| \geq |t_{0}| \} = 2 P \{ t(k) \geq |t_{0}| \}\]

其中 \(t_{0}\) 为给定样本值时检验统计量的取值。

我们称上述小样本情形下的检验为两样本近似 \(t\) 检验。

比较两个正态总体方差的假设检验

在前面有关两正态总体均值的比较问题中，当梁总体的方差未知时，我们首先需对两总体方差是否相等进行检验，即考虑下列假设问题：

\[H_{0}: \sigma_{1}^{2} = \sigma_{2}^{2}, H_{1}: \sigma_{1}^{2} \neq \sigma_{2}^{2}\]

取检验统计量为

\[F = \frac{S_{1}^{2}}{S_{2}^{2}}\]

当 \(H_{0}\) 成立时，\(F \sim F(n_{1} - 1, n_{2} - 1)\)，且此时 \(F\) 的取值既不能偏大也不能偏小，因此检验的拒绝域为

\[W = \{ F \geq F_{\frac{\alpha}{2}}(n_{1} - 1, n_{2} - 1) \text{ 或 } F \leq F_{1 - \frac{\alpha}{2}}(n_{1} - 1, n_{2} - 1) \}\]

记 \(f_{0} = \frac{s_{1}^{2}}{s_{2}^{2}}\) 为给定样本值时检验统计量的取值，设

\[p_{0} = P_{\sigma_{1}^{2} = \sigma_{2}^{2}} \left\{ \frac{S_{1}^{2}}{S_{2}^{2}} \leq \frac{s_{1}^{2}}{s_{2}^{2}} \right\} = P \{ F(n_{1} - 1, n_{2} - 1) \leq f_{0} \}\]

\(P\)-值为

\[P\text{-值} = 2 \min \{ p_{0}, 1 - p_{0} \}\]

类似地，对于左侧检验

\[H_{0}: \sigma_{1}^{2} \geq \sigma_{2}^{2}, H_{1}: \sigma_{1}^{2} < \sigma_{2}^{2}\]

\(P\)-值为

\[P\text{-值} = p_{0}\]

对于右侧检验

\[H_{0}: \sigma_{1}^{2} \leq \sigma_{2}^{2}, H_{1}: \sigma_{1}^{2} > \sigma_{2}^{2}\]

\(P\)-值为

\[P\text{-值} = 1 - p_{0}\]

正态总体参数的假设检验总结

我们将正态总体参数的假设检验整理为下表：

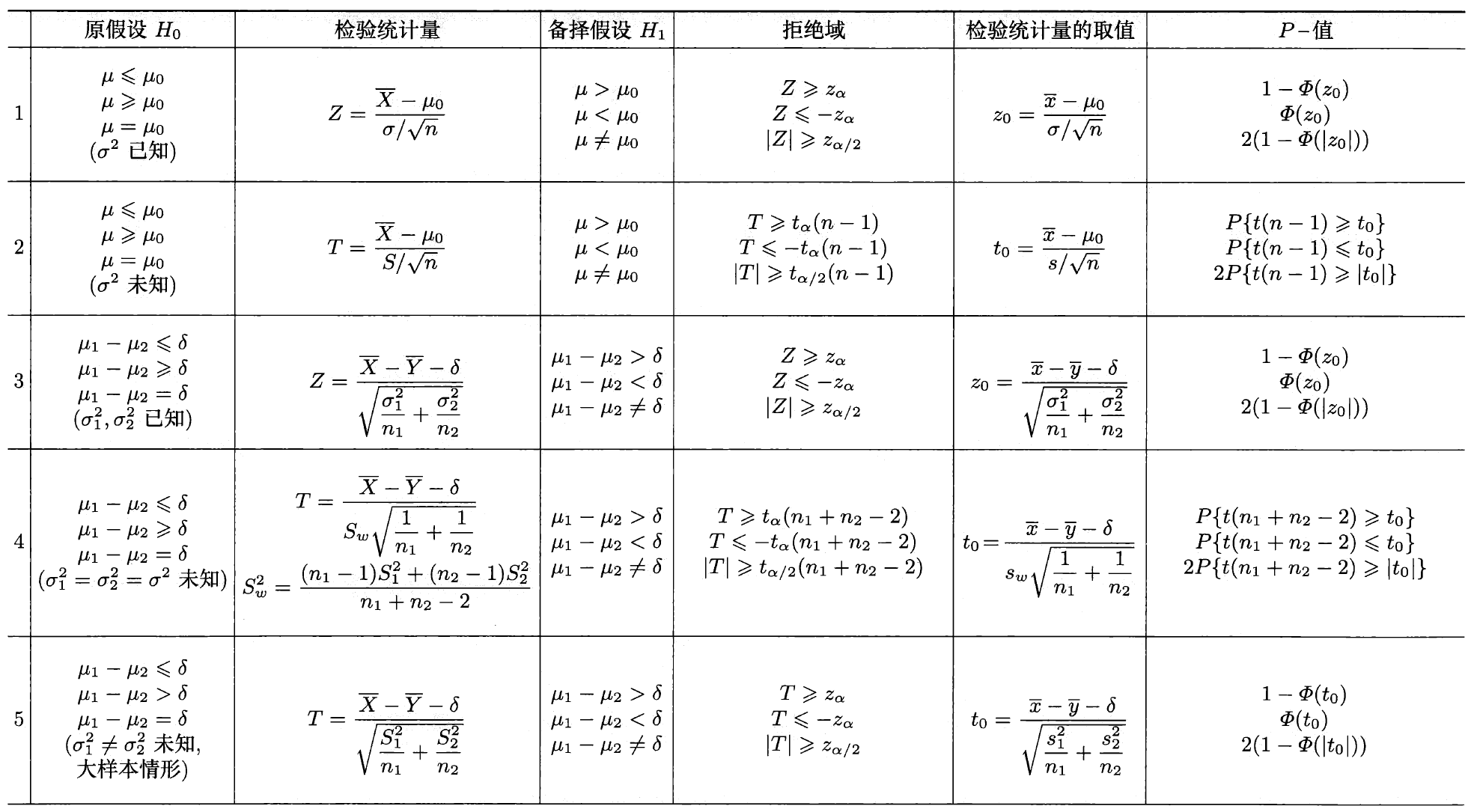
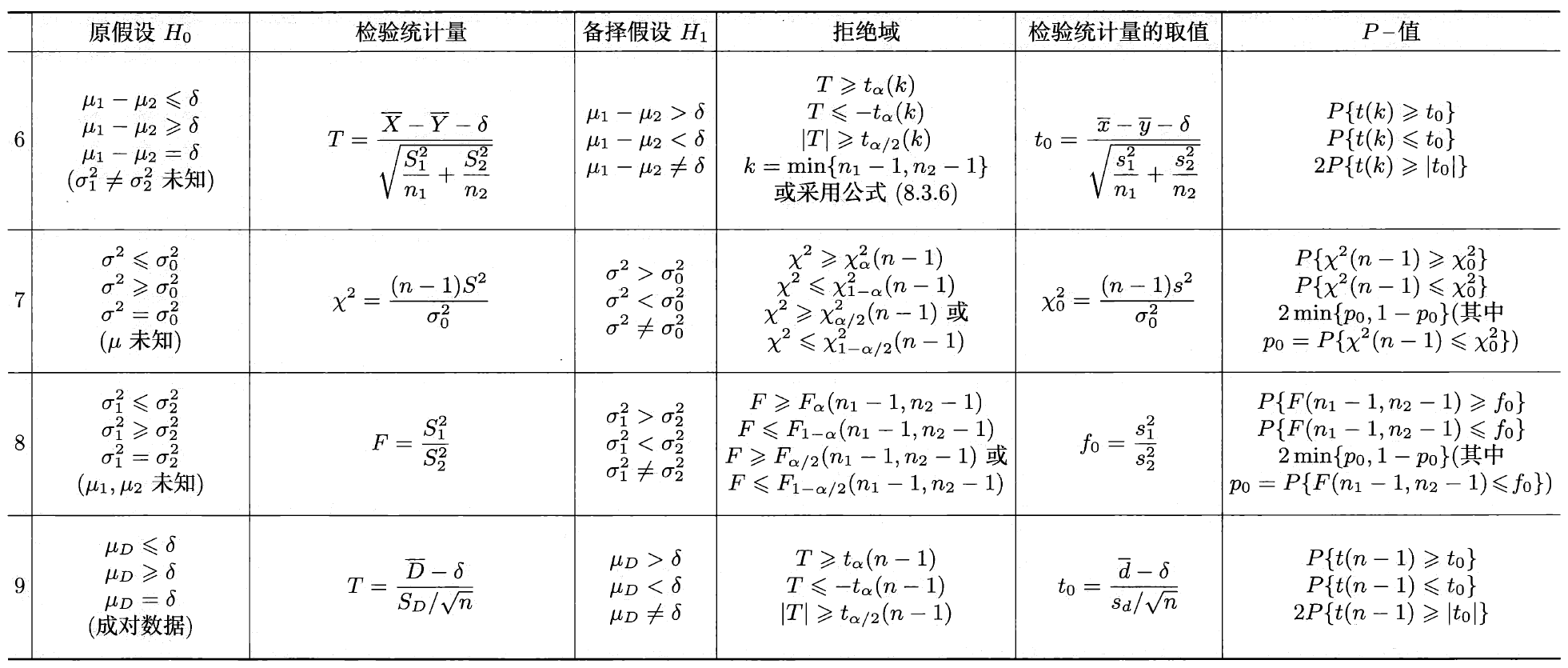
假设检验与区间估计

假设检验和区间估计间有密切的联系。

先来看方差已知时单个正态总体均值的假设检验与区间估计的关系。设 \(X_{1}, X_{2}, \cdots, X_{n}\) 时来自正态总体 \(N(\mu, \sigma^{2})\) 的样本，其中方差 \(\sigma^{2}\) 已知。根据前述讨论，可知 \(\mu\) 的置信水平为 \(1 - \alpha\) 的置信区间为

\[\left( \bar{X} - \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}}, \bar{X} + \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}} \right)\]

对于均值 \(\mu\) 的双侧假设问题

\[H_{0}: \mu = \mu_{0}, H_{1}: \mu \neq \mu_{0}\]

在给定的显著性水平下，检验的拒绝域为

\[W = \left\{ \left| \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}} \right| \geq z_{\frac{\alpha}{2}} \right\}\]

从而检验的接受域为

\[ \overline{W} = \left\{ \left| \frac{\bar{X} - \mu_{0}}{\frac{\sigma}{\sqrt{n}}} \right| < z_{\frac{\alpha}{2}} \right\} = \left\{ \bar{X} - \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}} < \mu_{0} < \bar{X} + \frac{\sigma}{\sqrt{n}}z_{\frac{\alpha}{2}} \right\}\]

可见，\(\mu\) 的置信水平为 \(1 - \alpha\) 的置信区间和 \(\mu\) 的显著性水平为 \(\alpha\) 的检验接受域可以互相推知。

一般来说，设 \(X_{1}, X_{2}, \cdots, X_{n}\) 为来自总体 \(X \sim F(x; \theta)\) 的样本。如果双侧假设问题

\[H_{0}: \theta = \theta_{0}, H_{1}: \theta \neq \theta_{0}\]

的显著性水平为 \(\alpha\) 的检验的接受域 \(\overline{W}\) 能等价地写成 \(\hat{\theta}_{L} < \theta < \hat{\theta}_{U}\) 的形式，那么 \((\hat{\theta}_{L}, \hat{\theta}_{U})\) 是 \(\theta\) 的置信水平为 \(1 - \alpha\) 的置信区间。反之，若 \((\hat{\theta}_{L}, \hat{\theta}_{U})\) 是 \(\theta\) 的置信水平为 \(1 - \alpha\) 的置信区间，则当 \(\theta_{0} \in (\hat{\theta}_{L}, \hat{\theta}_{U})\) 是，我们没有充分的把握认为 \(\theta \neq \theta_{0}\)，因此接受原假设 \(H_{0}: \theta = \theta_{0}\)。显然这个假设的拒绝域为

\[W = \{ \theta_{0} \leq \hat{\theta}_{L} \text{ 或 } \theta_{0} \geq \hat{\theta}_{U} \}\]

拟合优度检验

前面的讨论都是在总体服从正态分布的前提下，对分布的参数进行的假设检验。但在实际情况中，有时不能预知总体服从什么类型的分布，这时就需要现根据样本检验关于总体分布的假设。

设 \(F(x)\) 是总体的未知的分布函数，又设 \(F_{0}(x)\) 是具有某种已知类型的分布函数，但可能含有若干个位置参数，需检验假设

\[H_{0}: F(x) = F_{0}(x)\]

统计中有关这类分布的假设检验称作拟合优度检验。本节主要介绍皮尔逊拟合优度 \(\chi^{2}\) 检验。

皮尔逊 \(\chi^{2}\) 检验的基本思想：对总体 \(X\) 的取值分成互不相容的 \(k\) 类，记作 \(A_{1}, A_{2}, \cdots, A_{k}\)。设 \(X_{1}, X_{2}, \cdots, X_{n}\) 是来自该总体的样本，并记 \(n_{i}\) 为样本值落在 \(A_{i}\) 的个数。当 \(H_{0}\) 中的 \(F_{0}(x)\) 完全已知时，我们可以计算 \(p_{i} = P_{H_{0}}(A_{i}), i = 1, 2, \cdots, k\)。而当假设 \(H_{0}\) 中的 \(F_{0}(x)\) 含有 \(r\) 个位置参数时，要先在 \(F_{0}(x)\) 的形式下利用极大似然法估计 \(r\) 个未知的参数，然后求得 \(p_{i}\) 的估计 \(\hat{p}_{i}\)。当 \(H_{0}\) 为真时，\(n\) 个个体中属于 \(A_{i}\) 类的期望个数应为 \(np_{i}\)（或 \(n \hat{p}_{i}\)）。在统计中，\(n_{i}\) 称作实际频数，\(np_{i}\)（或 \(n \hat{p}_{i}\)）称作理论频数。皮尔逊提出用统计量

\[\chi^{2} = \sum_{i = 1}^{k} \frac{(n_{i} - np_{i})^{2}}{np_{i}}\]

或

\[\chi^{2} = \sum_{i = 1}^{k} \frac{(n_{i} - n \hat{p}_{i})^{2}}{n \hat{p}_{i}}\]

作为衡量实际频数与理论频数偏差的综合指标。皮尔逊证明了以下极限定理：

当 \(n\) 充分大时，若 \(H_{0}\) 为真，统计量 \(\chi^{2}\) 近似服从 \(chi^{2}(k - r - 1)\) 分布，其中 \(k\) 为分类数，\(r\) 为 \(F_{0}(x)\) 中含有的未知参数个数。

由当 \(H_{0}\) 为真时，\(\chi^{2}\) 的值偏小。故检验的拒绝域为

\[W = \{ \chi^{2} \geq \chi_{\alpha}^{2} (k - r - 1) \}\]

\(P\)-值为

\[P\text{-值} = P \{ \chi^{2}(k - r - 1) \geq \chi_{0}^{2} \}\]

其中 \(\chi_{0}^{2}\) 为检验统计量 \(\chi^{2}\) 的观测值。我们称 \(P\)-值为所得数据原假设的拟合优度。\(P\)-值越大，则越没有充分的理由拒绝原假设。给定显著性水平 \(\alpha\)，当 \(P\text{-值} \leq \alpha\) 时，就拒绝原假设。